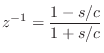Digitizing Elementary Reflectances by Bilinear Transform
Going to discrete time via the bilinear transform means making the substitution
 |
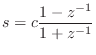(F.11) |
where
is an arbitrary real constant, usually taken to be 
.
Solving for 
gives us the inverse bilinear transform:
In this case, we see that setting 
further simplifies our
universal reflectances in the digital domain:
- For the ``wave digital capacitor'' (or spring), Eq.
(F.8) becomes
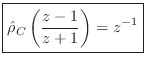
- For the ``wave digital inductor'' (or mass), Eq.(F.9) becomes
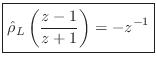
- And for the ``wave digital resistor'' (or dashpot), Eq.(F.10) becomes
as before in the continuous-time case.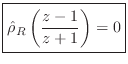
Note that this choice of 
is also the only one that eliminates
delay-free paths in the fundamental elements. This allows them to
be used as building blocks for explicit finite difference
schemes.
We may still obtain the above results using the more typical value
(instead of ) in the bilinear transform. From
Eq.(F.12), it is clear that changing amounts to a linear
frequency scaling of 
. Such a scaling may be compensated
by choosing the waveguide (port) impedances to be
(instead of 
) for the inductor, and
(instead of
) for the capacitor.
Next Section:
Compatible Port Connections
Previous Section:
Choosing Impedance to Simplify Element Reflectance
