DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Exact Reverb via Transfer-Function Modeling

Figure 3.1 depicts the general reverberation scenario for three sources and one listener (two ears). In general, the filters should also include filtering by the pinnae of the ears, so that each echo can be perceived as coming from the correct angle of arrival in 3D space; in other words, at least some reverberant reflections should be spatialized so that they appear to come from their natural directions in 3D space [248]. Again, the filters change if anything changes in the listening space, including source or listener position. The artificial reverberation problem is then to implement some approximation of the system in Fig.3.1.

Figure 3.1: General reverberation simulation for three sources and one listener (two ears). Each filter $ h_{ij}$ can be implemented as a tapped delay line FIR filter.
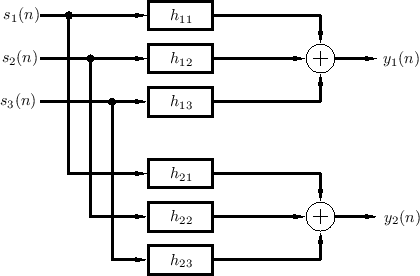\includegraphics{eps/reverb}

In the frequency domain, it is convenient to express the input-output relationship in terms of the transfer-function matrix:

$\displaystyle \left[\begin{array}{c} Y_1(z) \\ [2pt] Y_2(z) \end{array}\right] ... ...left[\begin{array}{c} S_1(z) \\ [2pt] S_2(z) \\ [2pt] S_3(z)\end{array}\right] $

Denoting the impulse response of the filter from source $ j$ to ear $ i$ by $ h_{ij}(n)$, the two output signals in Fig.3.1 are computed by six convolutions:

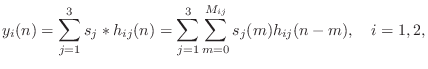
$\displaystyle y_i(n) = \sum_{j=1}^3 s_j \ast h_{ij}(n) = \sum_{j=1}^3 \sum_{m=0}^{M_{ij}} s_j(m)h_{ij}(n-m), \quad i=1,2, $

where $ M_{ij}$ denotes the order of FIR filter $ h_{ij}$. Since many of the filter coefficients $ h_{ij}(n)$ are zero (at least for small $ n$), it is more efficient to implement them as tapped delay lines (§2.5) so that the inner sum becomes sparse. For greater accuracy, each tap may include a lowpass filter which models air absorption [314] and/or spherical spreading loss (see §2.3). For large $ n$, the impulse responses are not sparse, and we must either implement very expensive FIR filters, or approximate the tail of the impulse response using less expensive IIR filters; this subject--``late reverberation'' approximation--is taken up in §3.4.

Next Section:
Complexity of Exact Reverberation
Previous Section:
Digital Waveguide Networks