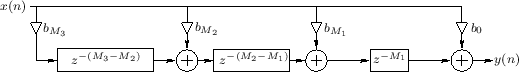DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Tapped Delay Line (TDL)

A tapped delay line (TDL) is a delay line with at least one ``tap''. A delay-line tap extracts a signal output from somewhere within the delay line, optionally scales it, and usually sums with other taps for form an output signal. A tap may be interpolating or non-interpolating. A non-interpolating tap extracts the signal at some fixed integer delay relative to the input. Thus, a tap implements a shorter delay line within a larger one, as shown in Fig.2.18.

Figure 2.18: A delay line with one tap.
\includegraphics{eps/tdlsimp}

Tapped delay lines efficiently simulate multiple echoes from the same source signal. As a result, they are extensively used in the field of artificial reverberation.

Example Tapped Delay Line

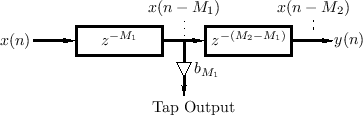
An example of a TDL with two internal taps is shown in Fig.2.19. The total delay line length is $ M_3$ samples, and the internal taps are located at delays of $ M_1$ and $ M_2$ samples, respectively. The output signal is a linear combination of the input signal $ x(n)$, the delay-line output $ x(n-M_3)$, and the two tap signals $ x(n-M_1)$ and $ x(n-M_2)$.

Figure 2.19: Tapped Delay Line (TDL).
\includegraphics{eps/tdl}

The difference equation of the TDL in Fig.2.19 is, by inspection,

$\displaystyle y(n) = b_0 x(n) + b_{M_1} x(n-M_1) + b_{M_2} x(n-M_2) + b_{M_3} x(n-M_3) $

corresponding to the transfer function

$\displaystyle H(z) = b_0 + b_{M_1} z^{-M_1} + b_{M_2} z^{-M_2} + b_{M_3} z^{-M_3} $

Transposed Tapped Delay Line

Figure 2.20: Transposed Tapped Delay Line (TTDL).
\includegraphics{eps/ttdl}

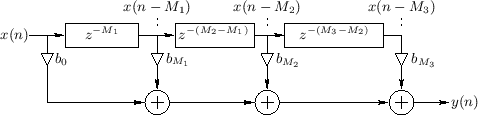
In many applications, the transpose of a tapped delay line is desired, as shown in Fig.2.20, which is the transpose of the tapped delay line shown in Fig.2.19. A transposed TDL is obtained from a normal TDL by formal transposition of the system diagram. The transposition operation is also called flow-graph reversal [333, pp. 153-155]. A flow-graph is transposed by reversing all signal paths, which necessitates signal branchpoints becoming sums, and sums becoming branchpoints. For single-input, single-output systems, the transfer function is the same, but the input and output are interchanged. This ``flow-graph reversal theorem'' derives from Mason's gain formula for signal flow graphs. Transposition is used to convert direct-forms I and II of a digital filter to direct-forms III and IV, respectively [333].

TDL for Parallel Processing

When multiplies and additions can be performed in parallel, the computational complexity of a tapped delay line is $ {\cal O}(1)$ multiplies and $ {\cal O}(\lg(K))$ additions, where $ K$ is the number of taps. This computational complexity is achieved by arranging the additions into a binary tree, as shown in Fig.2.21 for the case $ K=4$.

Figure 2.21: An example Tapped Delay Line (TDL), with additions organized into a binary tree for maximized parallel computation.
\includegraphics{eps/tdlbt}

General Causal FIR Filters

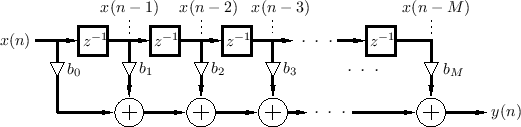
The most general case--a TDL having a tap after every delay element--is the general causal Finite Impulse Response (FIR) filter, shown in Fig.2.22. It is restricted to be causal because the output $ y(n)$ may not depend on ``future'' inputs $ x(n+1)$, $ x(n+2)$, etc. The FIR filter is also called a transversal filter. FIR filters are described in greater detail in [449].

Figure 2.22: The general, causal, finite-impulse-response (FIR) digital filter.
\includegraphics{eps/fir}

The difference equation for the $ M$th-order FIR filter in Fig.2.22 is, by inspection,

$\displaystyle y(n) = b_0 x(n) + b_1 x(n-1) + b_2 x(n-2) + b_3 x(n-3) + \cdots + b_M x(n-M) $

and the transfer function is

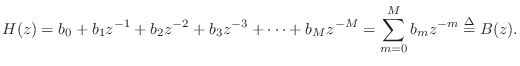
$\displaystyle H(z) = b_0 + b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3} + \cdots + b_M z^{-M} = \sum_{m=0}^M b_m z^{-m} \isdef B(z). $

The STK class for implementing arbitrary direct-form FIR filters is called Fir. (There is also a class for IIR filters named Iir.) In Matlab and Octave, the built-in function filter is normally used.

Next Section:
Comb Filters
Previous Section:
Digital Waveguides