Lossy Acoustic Propagation
Attenuation of waves by spherical spreading, as described in
§2.2.5 above, is not the only source of amplitude decay
in a traveling wave. In air, there is always significant additional
loss caused by air absorption. Air absorption varies with
frequency, with high frequencies usually being more attenuated than
low frequencies, as discussed in §B.7.15. Wave
propagation in vibrating strings undergoes an analogous
absorption loss, as does the propagation of nearly every other kind of
wave in the physical world. To simulate such propagation losses, we
can use a delay line in series with a nondispersive filter, as
illustrated in §2.2.2 above. In practice, the desired attenuation
at each frequency becomes the desired magnitude frequency-response of
the filter in Fig.2.4, and filter-design software
(typically matlab) is used to compute the filter coefficients to
approximate the desired frequency response in some optimal way. The
phase response may be linear, minimum, or left unconstrained when
damping-filter dispersion is not considered harmful. There is
typically a frequency-dependent weighting on the approximation error
corresponding to audio perceptual importance (e.g., the weighting ![]() is a simple example that increases accuracy at low frequencies).
Some filter-design methods are summarized in §8.6.
is a simple example that increases accuracy at low frequencies).
Some filter-design methods are summarized in §8.6.
Exponentially Decaying Traveling Waves
Let
![]() denote the decay factor associated with
propagation of a plane wave over distance
denote the decay factor associated with
propagation of a plane wave over distance ![]() at frequency
at frequency
![]() rad/sec. For an ideal plane wave, there is no ``spreading
loss'' (attenuation by
rad/sec. For an ideal plane wave, there is no ``spreading
loss'' (attenuation by ![]() ). Under uniform conditions, the
amount of attenuation (in dB) is proportional to the distance
traveled; in other words, the attenuation factors for two successive
segments of a propagation path are multiplicative:
). Under uniform conditions, the
amount of attenuation (in dB) is proportional to the distance
traveled; in other words, the attenuation factors for two successive
segments of a propagation path are multiplicative:
Frequency-independent air absorption is easily modeled in an acoustic simulation by making the substitution
Frequency-Dependent Air-Absorption Filtering
More generally, frequency-dependent air absorption can be modeled using the substitution
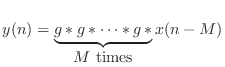
For spherical waves, the loss due to spherical spreading is of the form
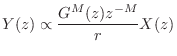
Dispersive Traveling Waves
In addition to frequency-dependent attenuation, LTI filters can provide a frequency-dependent delay. This can be used to simulate dispersive wave propagation, as introduced in §2.2.3.
Summary
Up to now, we have been concerned with the simulation of
traveling waves in linear, time-invariant (LTI) media.
The main example considered was wave propagation in air, but waves on
vibrating strings behave analogously. We saw that the point-to-point
propagation of a traveling plane wave in an LTI medium can be
simulated simply using only a delay line and an LTI
filter. The delay line simulates propagation delay, while the filter
further simulates (1) an independent attenuation factor at each
frequency by means of its amplitude response (e.g., to simulate air
absorption), and (2) a frequency-dependent propagation speed using its
phase response (to simulate dispersion). If there is additionally
spherical spreading loss, the amplitude may be further attenuated by
![]() , where
, where ![]() is the distance from the source. For more details
about the acoustics of plane waves and spherical waves, see, e.g.,
[318,349]. Appendix B contains a bit more about
elementary acoustics,
is the distance from the source. For more details
about the acoustics of plane waves and spherical waves, see, e.g.,
[318,349]. Appendix B contains a bit more about
elementary acoustics,
So far we have considered only traveling waves going in one direction. The next simplest case is 1D acoustic systems, such as vibrating strings and acoustic tubes, in which traveling waves may propagate in two directions. Such systems are simulated using a pair of delay lines called a digital waveguide.
Next Section:
Digital Waveguides
Previous Section:
Acoustic Wave Propagation Simulation



















