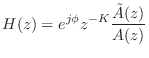Example Allpass Filters
- The simplest allpass filter is a unit-modulus gain
where
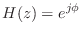
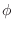 can be any phase value. In the real case
can be any phase value. In the real case 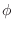 can only be 0 or
can only be 0 or 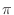 , in which case
, in which case
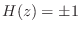 .
.
- A lossless FIR filter can consist only of a single nonzero tap:
for some fixed integer
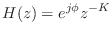
 , where
, where 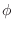 is again some constant phase,
constrained to be 0 or
is again some constant phase,
constrained to be 0 or 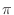 in the real-filter case. Since we are
considering only causal filters here,
in the real-filter case. Since we are
considering only causal filters here, 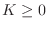 . As a special case of
this example, a unit delay
. As a special case of
this example, a unit delay
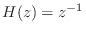 is a simple FIR allpass filter.
is a simple FIR allpass filter.
- The transfer function of every finite-order, causal,
lossless IIR digital filter (recursive allpass filter) can be written as
where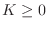 ,
,
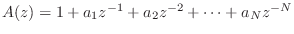 , and
, and
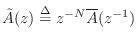 . The polynomial
. The polynomial
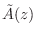 can be obtained by reversing the order of the coefficients in
can be obtained by reversing the order of the coefficients in
 and conjugating them. (The factor
and conjugating them. (The factor 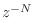 serves to restore
negative powers of
serves to restore
negative powers of  and hence causality.)
and hence causality.)
Next Section:
Gerzon Nested MIMO Allpass
Previous Section:
More General Allpass Filters