DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

More General Allpass Filters

We have so far seen two types of allpass filters:

  • The series combination of feedback and feedforward comb-filters is allpass when their delay lines are the same length and their feedback and feedforward coefficents are the same. An example is shown in Fig.2.30.
  • Any delay element in an allpass filter can be replaced by an allpass filter to obtain a new (typically higher order) allpass filter. The special case of nested first-order allpass filters yielded the lattice digital filter structure of Fig.2.32.
We now discuss allpass filters more generally in the SISO case. (See Appendix D of [449] for the MIMO case.)


Definition: A linear, time-invariant filter $ H(z)$ is said to be lossless if it preserves signal energy for every input signal. That is, if the input signal is $ x(n)$, and the output signal is $ y(n) = (h\ast x)(n)$, we must have

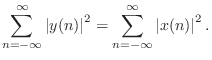
$\displaystyle \sum_{n=-\infty}^{\infty} \left\vert y(n)\right\vert^2 = \sum_{n=-\infty}^{\infty} \left\vert x(n)\right\vert^2. $

In terms of the $ L2$ signal norm $ \left\Vert\,\,\cdot\,\,\right\Vert _2$, this can be expressed more succinctly as

$\displaystyle \left\Vert\,y\,\right\Vert _2^2 = \left\Vert\,x\,\right\Vert _2^2. $

Notice that only stable filters can be lossless since, otherwise, $ \left\Vert\,y\,\right\Vert$ is generally infinite, even when $ \left\Vert\,x\,\right\Vert$ is finite. We further assume all filters are causal3.14 for simplicity. It is straightforward to show the following:

It can be shown [449, Appendix C] that stable, linear, time-invariant (LTI) filter transfer function $ H(z)$ is lossless if and only if

$\displaystyle \left\vert H(e^{j\omega})\right\vert = 1, \quad \forall \omega. $

That is, the frequency response must have magnitude 1 everywhere over the unit circle in the complex $ z$ plane.

Thus, ``lossless'' and ``unity-gain allpass'' are synonymous. For an allpass filter with gain $ g$ at each frequency, the energy gain of the filter is $ g^2$ for every input signal $ x$. Since we can describe such a filter as an allpass times a constant gain, the term ``allpass'' will refer here to the case $ g=1$.

Next Section:
Example Allpass Filters
Previous Section:
Nested Allpass Filters