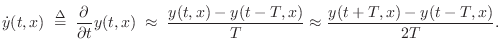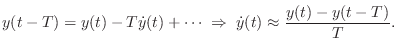Finite Difference Methods
One of the first applications of digital computers to numerical
simulation of physical systems was the so-called finite
difference approach [481].
The general
procedure is to replace derivatives by finite differences, and there
are many variations on how this can be done. For example, the first
partial derivative with respect to time in Eq.![]() (A.1) may be
approximated by
(A.1) may be
approximated by
The second form, called a centered finite difference, has the advantage of not introducing a time delay, but at the expense of requiring an extra factor of two oversampling for a given accuracy in its magnitude response (when viewed as a digital filter).
Finite differences are at least as old as Taylor series, since,
Interestingly, the general Taylor series, published in 1715 by Taylor in his book Methodus Incrementorum Directa et Inversa, was known more than forty years earlier to James Gregory (1668), somewhat earlier to Jean Bernoulli, and to some extent even before 1550 in India [65, pp. 422,469].
Finite differences were used to construct the earliest known digital models of vibrating strings by Pierre Ruiz and Lejaren Hiller ca. 1971 [194].
Finite-difference methods have not historically been aimed at real-time simulation, and they are generally used with very large sampling rates compared with the ``band of interest''. On the order of ten-times oversampling is needed to obtain reasonably accurate simulation across the entire audio band when using classical finite difference methods. In the finite-difference method literature, accuracy is usually only considered at dc, which is inaudible. Since finite difference models are usually linear, time-invariant digital filters, it is straightforward to improve them by filter-design methods, optimizing perceived audio error over the entire audio band. Such improved (and optionally extended) coefficients can then be used to construct a refined, indirectly estimated, partial differential equation.
Other offline (slower than real time) computational physical modeling methods include finite element [480] and boundary element methods. Such offline simulations can be valuable as a source of ``virtual experiments'' which enable the testing and calibration of faster algorithms. As an example, a detailed simulation of guitar acoustics, employing both finite difference and finite element modeling approaches, is reported in [109].
Next Section:
Transfer Function Models
Previous Section:
Analog Computers