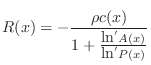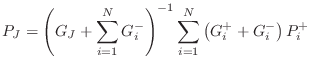Free Books
   Free Books    Physical Audio Signal Processing  

Generalized Scattering Coefficients

Generalizing the scattering coefficients at a multi-tube intersection (§C.12) by replacing the usual real tube wave impedance 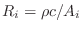$ R_i=\rho c/A_i$ by the complex generalized wave impedance

$\displaystyle R(x)=-\frac{\rho c(x)}{1 + \frac{\mbox{ln}'A(x)}{\mbox{ln}'P(x)}} $

from Eq.$ \,$(C.152), or, as a special case, the conical-section wave impedance $ R_A^\pm (s)=[\rho c/A(x)]/[s/(s \pm 1/t_x)]$ from Eq.$ \,$(C.151), we obtain the junction-pressure phasor [436]

$\displaystyle P_J = \left(G_J + \sum_{i=1}^N G_i^-\right)^{-1} \sum_{i=1}^N \left(G_i^+ + G_i^- \right)P_i^+ $

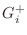
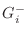
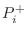
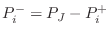
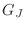
where $ G_i^+ $ is the complex, frequency-dependent, incoming, acoustic admittance of the $ i$th branch at the junction, $ G_i^-$ is the corresponding outgoing acoustic admittance, $ P_i^+$ is the incoming traveling pressure-wave phasor in branch $ i$, $ P_i^- = P_J - P_i^+$ is the outgoing wave, and $ G_J$ is the admittance of a load at the junction, such as a coupling to another simulation. For generality, the formula is given as it appears in the multivariable case.

Next Section:
Cylinder with Conical Cap
Previous Section:
Generalized Wave Impedance