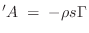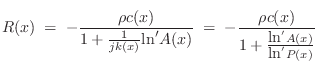More General One-Parameter Waves
The wave impedance derivation above made use of known properties of waves
in cones to arrive at the wave impedances in the two directions of travel
in cones. We now consider how this solution might be generalized to
arbitrary bore shapes. The momentum conservation equation is already
applicable to any wavefront area variation  :
:
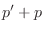
ln

As we did for
vibrating strings (§
C.3.4), suppose the
pressure is sinusoidally driven so that we have
where
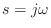
,
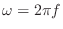
, and

is the driving frequency.
The partial derivatives become
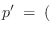
ln

Substituting into the
momentum equation gives
Because the medium is
linear and time-invariant, the
velocity 
must
be of the form
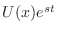
, and we can define the spatially instantaneous
wave impedance as
The corresponding instantaneous wave
admittance is then
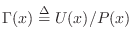
.
Then
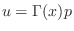
, and the momentum equation becomes
ln
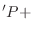
ln
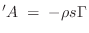
Solving for the wave
impedance gives
Expressing
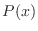
in
exponential form as
where
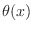
may be complex, we may define the instantaneous
spatial frequency (wavenumber) as
and since
ln
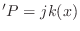
, we have
Defining the spatially instantaneous phase velocity as
we have
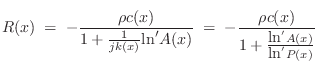 |
(C.151) |
This reduces to the simple case of the uniform
waveguide when the
logarithmic derivative of
cross-sectional area 
is small compared
with the logarithmic derivative of the amplitude
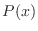
which
is proportional to the instantaneous spatial frequency.
A
traveling wave solution interpretation makes sense when
the instantaneous wavenumber
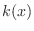
is approximately real, and
the phase velocity
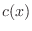
is approximately constant over a number of
wavelengths
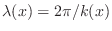
.
Next Section: Generalized Wave ImpedancePrevious Section: Wave Impedance in a Cone
![]() :
:
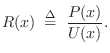
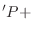 ln
ln