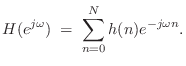In fractional-delay filtering
applications, the interpolator
typically slides forward through time to produce a time series of
interpolated values, thereby implementing a non-integer signal delay:
where
![$ \eta\in[-1/2,1/2]$](http://www.dsprelated.com/josimages_new/pasp/img1019.png)
spans the central one-sample range of the
interpolator. Equivalently, the interpolator may be viewed as an
FIR
filter having a linear
phase response corresponding to a delay of
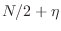
samples. Such filters are often used in series with a
delay
line in order to implement an
interpolated delay line
(§
4.1) that effectively provides a continuously
variable delay for discrete-time signals.
The frequency response [449] of the fractional-delay
FIR filter 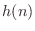 is
is
For an ideal fractional-delay filter, the frequency response should be
equal to that of an ideal delay
where

denotes the total desired delay of
the filter. Thus, the ideal desired frequency response is a
linear
phase term corresponding to a delay of

samples.
Next Section: Lagrange Interpolation OptimalityPrevious Section: Interpolation of Uniformly Spaced Samples
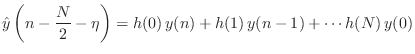
![]() is
is