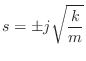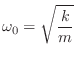DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Oscillation Frequency

From Fig.F.33, we can see that the impedance of the parallel combination of the mass and spring is given by

$\displaystyle R_{m\vert\vert k}(s) \isdef \left.\frac{k}{s} \right\Vert ms = \frac{\frac{k}{s}ms}{\frac{k}{s}+ms} = \frac{ks}{s^2+\frac{k}{m}} \protect$ (F.38)

(using the product-over-sum rule for combining impedances in parallel). The poles of this impedance are given by the roots of the denominator polynomial in $ s$:

$\displaystyle s = \pm j\sqrt{\frac{k}{m}} \protect$ (F.39)

The resonance frequency of the mass-spring oscillator is therefore

$\displaystyle \omega_0 = \sqrt{\frac{k}{m}} \protect$ (F.40)

Since the poles $ s=\pm j\omega_0$ are on the $ j\omega $ axis, there is no damping, as we expect.

We can now write reflection coefficient $ \rho$ (see Fig.F.35) as

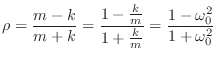
$\displaystyle \rho = \frac{m-k}{m+k} = \frac{1-\frac{k}{m}}{1+\frac{k}{m}} = \frac{1-\omega_0^2}{1+\omega_0^2} $

We see that dc ( $ \omega_0=0$) corresponds to $ \rho=1$, and $ \omega_0=\infty$ corresponds to $ \rho=-1$.

Next Section:
DC Analysis of the WD Mass-Spring Oscillator
Previous Section:
Checking the WDF against the Analog Equivalent Circuit