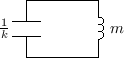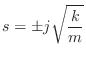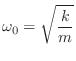Wave Digital Mass-Spring Oscillator
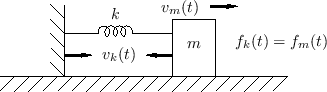
Let's look again at the mass-spring oscillator of §F.3.4, but this time without the driving force (which effectively decouples the mass and spring into separate first-order systems). The physical diagram and equivalent circuit are shown in Fig.F.32 and Fig.F.33, respectively.
Note that the mass and spring can be regarded as being in parallel or
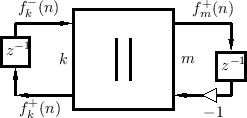
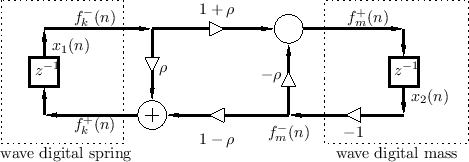
in series. Under the parallel interpretation, we have the WDF shown
in Fig.F.34 and Fig.F.35.F.5
The reflection coefficient ![]() can be computed, as usual, from
the first alpha parameter:
can be computed, as usual, from
the first alpha parameter:
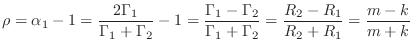
Oscillation Frequency
From Fig.F.33, we can see that the impedance of the parallel combination of the mass and spring is given by
(using the product-over-sum rule for combining impedances in parallel). The poles of this impedance are given by the roots of the denominator polynomial in
The resonance frequency of the mass-spring oscillator is therefore
Since the poles
We can now write reflection coefficient ![]() (see Fig.F.35) as
(see Fig.F.35) as
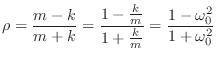
DC Analysis of the WD Mass-Spring Oscillator
Considering the dc case first (![]() ), we see from Fig.F.35
that the state variable
), we see from Fig.F.35
that the state variable ![]() will circulate unchanged in the
isolated loop on the left. Let's call this value
will circulate unchanged in the
isolated loop on the left. Let's call this value
![]() . Then the physical force on the spring is always equal to
. Then the physical force on the spring is always equal to
The loop on the right in Fig.F.35 receives
At first, this result might appear to contradict conservation of energy, since the state amplitude seems to be growing without bound. However, the physical force is fortunately better behaved:
Since the spring and mass are connected in parallel, it must be the true that they are subjected to the same physical force at all times. Comparing Equations (F.41-F.43) verifies this to be the case.
WD Mass-Spring Oscillator at Half the Sampling Rate
Under the bilinear transform, the ![]() maps to
maps to ![]() (half the
sampling rate). It is therefore no surprise that given
(half the
sampling rate). It is therefore no surprise that given
![]() (
(![]() ), inspection of Fig.F.35 reveals
that any alternating sequence (sinusoid sampled at half the sampling
rate) will circulate unchanged in the loop on the right, which is now
isolated. Let
), inspection of Fig.F.35 reveals
that any alternating sequence (sinusoid sampled at half the sampling
rate) will circulate unchanged in the loop on the right, which is now
isolated. Let
![]() denote this alternating sequence.
The loop on the left receives
denote this alternating sequence.
The loop on the left receives
![]() and adds
and adds
![]() to
it, i.e.,
to
it, i.e.,
![]() .
If we start out with
.
If we start out with ![]() and
and
![]() , we obtain
, we obtain
![]() , or
, or
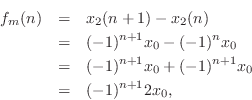
which agrees with the spring, as it must.
Linearly Growing State Variables in WD Mass-Spring Oscillator
It may seem disturbing that such a simple, passive, physically
rigorous simulation of a mass-spring oscillator should have to make
use of state variables which grow without bound for the limiting cases
of simple harmonic motion at frequencies zero and half the sampling
rate. This is obviously a valid concern in practice as well.
However, it is easy to show that this only happens at dc and ![]() ,
and that there is a true degeneracy at these frequencies, even in the
physics. For all frequencies in the audio range (e.g., for typical
sampling rates), such state variable growth cannot occur. Let's take
closer look at this phenomenon, first from a signal processing point
of view, and second from a physical point of view.
,
and that there is a true degeneracy at these frequencies, even in the
physics. For all frequencies in the audio range (e.g., for typical
sampling rates), such state variable growth cannot occur. Let's take
closer look at this phenomenon, first from a signal processing point
of view, and second from a physical point of view.
A Signal Processing Perspective on Repeated Mass-Spring Poles
Going back to the poles of the mass-spring system in Eq.![]() (F.39),
we see that, as the imaginary part of the two poles,
(F.39),
we see that, as the imaginary part of the two poles,
![]() , approach zero, they come together at
, approach zero, they come together at ![]() to create a
repeated pole. The same thing happens at
to create a
repeated pole. The same thing happens at
![]() since
both poles go to ``the point at infinity''.
since
both poles go to ``the point at infinity''.
It is a well known fact from linear systems theory that two poles at
the same point
![]() in the
in the ![]() plane can correspond to an
impulse-response component of the form
plane can correspond to an
impulse-response component of the form
![]() , in addition
to the component
, in addition
to the component
![]() produced by a single pole at
produced by a single pole at
![]() . In the discrete-time case, a double pole at
. In the discrete-time case, a double pole at ![]() can
give rise to an impulse-response component of the form
can
give rise to an impulse-response component of the form ![]() .
This is the fundamental source of the linearly growing internal states
of the wave digital sine oscillator at dc and
.
This is the fundamental source of the linearly growing internal states
of the wave digital sine oscillator at dc and ![]() . It is
interesting to note, however, that such modes are always
unobservable at any physical output such as the mass
force or spring force that is not actually linearly growing.
. It is
interesting to note, however, that such modes are always
unobservable at any physical output such as the mass
force or spring force that is not actually linearly growing.
Physical Perspective on Repeated Poles in the Mass-Spring System
In the physical system, dc and infinite frequency are in fact strange
cases. In the case of dc, for example, a nonzero constant force
implies that the mass ![]() is under constant acceleration. It is
therefore the case that its velocity is linearly growing. Our
simulation predicts this, since, using
Eq.
is under constant acceleration. It is
therefore the case that its velocity is linearly growing. Our
simulation predicts this, since, using
Eq.![]() (F.43) and Eq.
(F.43) and Eq.![]() (F.42),
(F.42),
![\begin{eqnarray*}
v_m(n) &=& \frac{f^{{+}}_m(n)}{m} - \frac{f^{{-}}_m(n)}{m}
=...
...m} \left[2(n+1) + 2n\right]x_0
= \frac{1}{m} (4 n x_0 + 2 x_0).
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img5032.png)
The dc term ![]() is therefore accompanied by a linearly growing
term
is therefore accompanied by a linearly growing
term ![]() in the physical mass velocity. It is therefore
unavoidable that we have some means of producing an unbounded,
linearly growing output variable.
in the physical mass velocity. It is therefore
unavoidable that we have some means of producing an unbounded,
linearly growing output variable.
Mass-Spring Boundedness in Reality
To approach the limit of
![]() , we must either
take the spring constant
, we must either
take the spring constant ![]() to zero, or the mass
to zero, or the mass ![]() to infinity, or
both.
to infinity, or
both.
In the case of ![]() , the constant force must approach zero, and we
are left with at most a constant mass velocity in the limit (not a
linearly growing one, since there can be no dc force at the limit).
When the spring force reaches zero,
, the constant force must approach zero, and we
are left with at most a constant mass velocity in the limit (not a
linearly growing one, since there can be no dc force at the limit).
When the spring force reaches zero, ![]() , so that only zeros
will feed into the loop on the right in Fig.F.35, thus avoiding
a linearly growing velocity, as demanded by the physics. (A constant
velocity is free to circulate in the loop on the right, but the loop
on the left must be zeroed out in the limit.)
, so that only zeros
will feed into the loop on the right in Fig.F.35, thus avoiding
a linearly growing velocity, as demanded by the physics. (A constant
velocity is free to circulate in the loop on the right, but the loop
on the left must be zeroed out in the limit.)
In the case of
![]() , the mass becomes unaffected by the spring
force, so its final velocity must be zero. Otherwise, the attached
spring would keep compressing or stretching forever, and this would
take infinite energy. (Another way to arrive at this conclusion is to
note that the final kinetic energy of the mass would be
, the mass becomes unaffected by the spring
force, so its final velocity must be zero. Otherwise, the attached
spring would keep compressing or stretching forever, and this would
take infinite energy. (Another way to arrive at this conclusion is to
note that the final kinetic energy of the mass would be
![]() .) Since the total energy in an undriven mass-spring
oscillator is always constant, the infinite-mass limit must be
accompanied by a zero-velocity limit.F.6 This means the mass's
state variable
.) Since the total energy in an undriven mass-spring
oscillator is always constant, the infinite-mass limit must be
accompanied by a zero-velocity limit.F.6 This means the mass's
state variable ![]() in Fig.F.35 must be forced to zero in
the limit so that there will be no linearly growing solution at dc.
in Fig.F.35 must be forced to zero in
the limit so that there will be no linearly growing solution at dc.
In summary, when two or more system poles approach each other to form
a repeated pole, care must be taken to ensure that the limit is
approached in a physically meaningful way. In the case of the
mass-spring oscillator, for example, any change in the spring constant
![]() or mass
or mass ![]() must be accompanied by the physically appropriate
change in the state variables
must be accompanied by the physically appropriate
change in the state variables ![]() and/or
and/or ![]() . It is
obviously incorrect, for example, to suddenly set
. It is
obviously incorrect, for example, to suddenly set ![]() in the
simulation without simultaneously clearing the spring's state variable
in the
simulation without simultaneously clearing the spring's state variable
![]() , since the force across an infinitely compliant spring can
only be zero.
, since the force across an infinitely compliant spring can
only be zero.
Similar remarks apply to repeated poles corresponding to
![]() . In this case, the mass and spring basically change
places.
. In this case, the mass and spring basically change
places.
Energy-Preserving Parameter Changes (Mass-Spring Oscillator)
If the change in ![]() or
or ![]() is deemed to be ``internal'', that is,
involving no external interactions, the appropriate accompanying
change in the internal state variables is that which conserves
energy. For the mass and its velocity, for example, we must have
is deemed to be ``internal'', that is,
involving no external interactions, the appropriate accompanying
change in the internal state variables is that which conserves
energy. For the mass and its velocity, for example, we must have
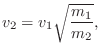
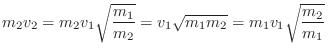
If the spring constant ![]() is to change from
is to change from ![]() to
to ![]() , the
instantaneous spring displacement
, the
instantaneous spring displacement ![]() must satisfy
must satisfy
Exercises in Wave Digital Modeling
- Comparing digital and analog frequency formulas.
This first exercise verifies that the elementary ``tank circuit''
always resonates at exactly the frequency it should, according to the
bilinear transform frequency mapping
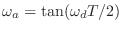 , where
, where 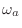 denotes ``analog frequency'' and
denotes ``analog frequency'' and 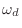 denotes ``digital frequency''.
denotes ``digital frequency''.
- Find the poles of Fig.F.35 in terms of
 .
.
- Show that the resonance frequency is given by
where
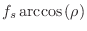
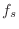 denotes the sampling rate.
denotes the sampling rate.
- Recall that the mass-spring oscillator resonates at
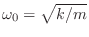 . Relate these two resonance frequency formulas
via the analog-digital frequency map
. Relate these two resonance frequency formulas
via the analog-digital frequency map
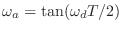 .
.
- Show that the trig identity you discovered in this way is true.
I.e., show that
![$\displaystyle f_s \arccos\left[\frac{k-m}{k+m}\right] =
2f_s \arctan\left[\sqrt{\frac{m}{k}}\right].
$](http://www.dsprelated.com/josimages_new/pasp/img5051.png)
- Find the poles of Fig.F.35 in terms of
Previous Section:
Mass and Dashpot in Series