DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Checking the WDF against the Analog Equivalent Circuit

Let's check our result by comparing the transfer function from the input force to the force on the mass in both the discrete- and continuous-time cases.

For the discrete-time case, we have

$\displaystyle H_m(z) \isdef \frac{F_3(z)}{F(z)} = \frac{F^{+}_3(z) + F^{-}_3(z)}{F(z)} = (1-z^{-1}) \frac{F^{-}_3(z)}{F(z)} $

where the last simplification comes from the mass reflectance relation $ F^{+}_3(z) = -z^{-1}F^{-}_3(z)$. (Note that we are using the standard traveling-wave notation for the adaptor, so that the $ \pm$ signs are swapped relative to element-centric notation.)

We now need $ F^{-}_3(z)/F(z)$. To simplify notation, define the two coefficients as

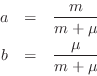
\begin{eqnarray*} a &=& \frac{m}{m+\mu}\\ b &=& \frac{\mu}{m+\mu} \end{eqnarray*}

From Figure F.30, we can write

\begin{eqnarray*} F^{-}_3(z) &=& -a\left[F(z)-z^{-1}F^{-}_3(z)\right] + b\left[-... ...\,\,\quad F^{-}_3(z) &=& -a\frac{F(z)}{1-(a-b)z^{-1}F^{-}_3(z)} \end{eqnarray*}

Thus, the desired transfer function is

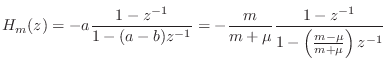
$\displaystyle H_m(z) = -a \frac{1-z^{-1}}{1-(a-b)z^{-1}} = -\frac{m}{m+\mu} \frac{1-z^{-1}}{1-\left(\frac{m-\mu}{m+\mu}\right)z^{-1}} $

We now wish to compare this result to the bilinear transform of the corresponding analog transfer function. From Figure F.27, we can recognize the mass and dashpot as voltage divider:

$\displaystyle H^a_m(s) = \frac{ms}{ms+\mu} $

Applying the bilinear transform yields

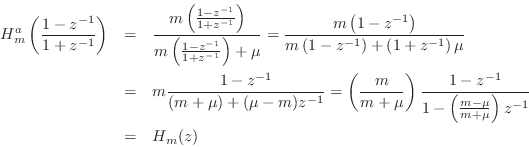
\begin{eqnarray*} H^a_m\left(\frac{1-z^{-1}}{1+z^{-1}}\right) &=& \frac{m\left(\... ...{-1}}{1 - \left(\frac{m-\mu}{m+\mu}\right)z^{-1}}\\ &=& H_m(z) \end{eqnarray*}

Thus, we have verified that the force transfer-function from the driving force to the mass is identical in the discrete- and continuous-time models, except for the bilinear transform frequency warping in the discrete-time case.

Next Section:
Oscillation Frequency
Previous Section:
A More Formal Derivation of the Wave Digital Force-Driven Mass