The second method is based on constructing a partial fraction expansion of
the admittance directly:
with
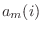
as above. While such a construction is not guaranteed to be
positive real, (please feel free to find general conditions for which the
positive-real condition can be guaranteed), we now have direct control over
the
bandwidths and modal gains (
pole residues in the admittance). The
reason the construction
tends to be positive real is that by using
the same phase for each section (the 1 in all the section numerators), we
are sure to get a zero forming at some frequency near the middle between
the resonance frequencies, and at a similar distance from the unit circle.
This means we are constructing interlacing
poles and zeros by simply adding
the
resonators in parallel. The extra zero near
dc is to ensure that
the admittance looks like a lightly damped
spring at zero frequency. Since
half the
sampling rate merely ``cuts off'' the
frequency response, there is
no corresponding requirement to add a pole near

as if it were the
point at infinity. However, the phase should be checked not to exceed plus
or minus
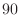
degrees there (or at any other frequency), and a pole or zero
added if necessary to pull it into the positive-real range.
A simple example of a synthetic bridge constructed using this method
with is shown in Fig.9.11.
Next Section: Matlab for Passive Reflectance Synthesis Method 1Previous Section: Passive Reflectance Synthesis--Method 1
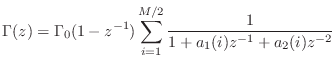








![\includegraphics[width=\twidth]{eps/lguitarsynth2}](http://www.dsprelated.com/josimages_new/pasp/img2031.png)












