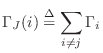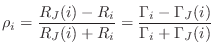DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Physical Derivation of Reflection Coefficient

Physically, the reflection coefficient seen at port $ i$ is due to an impedance step from $ R_i$, that of the port interface, to a new impedance consisting of the parallel combination of all other port impedances meeting at the junction. Let

$\displaystyle \Gamma _J(i) \isdef \sum_{i\neq j} \Gamma _i \protect$ (F.24)

denote this parallel combination, in admittance form. Then we must have

$\displaystyle \rho_i = \frac{R_J(i)-R_i}{R_J(i)+R_i} = \frac{\Gamma _i-\Gamma _J(i)}{\Gamma _i+\Gamma _J(i)} \protect$ (F.25)

Let's check this ``physical'' derivation against the formal definition Eq.$ \,$(F.20) leading to $ \rho_i = \alpha_i - 1$ in Eq.$ \,$(F.22). Toward this goal, let

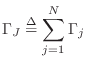
$\displaystyle \Gamma _J \isdef \sum_{j=1}^N \Gamma _j $

denote the parallel combination of all admittances connected to the junction. Then by Eq.$ \,$(F.24), we have $ \Gamma _J = \Gamma _i + \Gamma _J(i)$ for all $ i$. Now, from Eq.$ \,$(F.17),

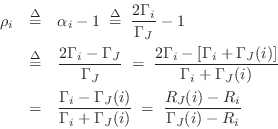
\begin{eqnarray*} \rho_i &\isdef & \alpha_i - 1 \;\isdef \; \frac{2\Gamma _i}{\... ..._i + \Gamma _J(i)} \;=\; \frac{R_J(i) - R_i}{\Gamma _J(i)-R_i} \end{eqnarray*}

and the result is verified.

Next Section:
Reflection Free Port
Previous Section:
Reflection Coefficient, Parallel Case