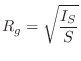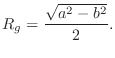DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Radius of Gyration

For a planar distribution of mass rotating about some axis in the plane of the mass, the radius of gyration is the distance from the axis that all mass can be concentrated to obtain the same mass moment of inertia. Thus, the radius of gyration is the ``equivalent distance'' of the mass from the axis of rotation. In this context, gyration can be defined as rotation of a planar region about some axis lying in the plane.

For a bar cross-section with area $ S$, the radius of gyration is given by

$\displaystyle R_g = \sqrt{\frac{I_S}{S}} \protect$ (B.11)

where $ I_S$ is the area moment of inertia (§B.4.8) of the cross-section about a given axis of rotation lying in the plane of the cross-section (usually passing through its centroid):

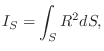
$\displaystyle I_S = \int_S R^2 dS, $

where $ R$ denotes the distance of the differential area element $ dS$ from the axis of gyration.

Rectangular Cross-Section

For a rectangular cross-section of height $ h$ and width $ w$, area $ S=hw$, the area moment of inertia about the horizontal midline is given by

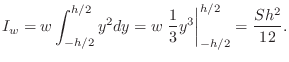
$\displaystyle I_w = w\int_{-h/2}^{h/2} y^2 dy = w\left.\frac{1}{3}y^3\right\vert _{-h/2}^{h/2} = \frac{Sh^2}{12}. $

The radius of gyration about this axis is then

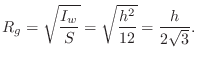
$\displaystyle R_g = \sqrt{\frac{I_w}{S}} = \sqrt{\frac{h^2}{12}} = \frac{h}{2\sqrt{3}}. $

Similarly, the radius of gyration about a vertical axis passing through the center of the cross-section is $ R_g=w/(2\sqrt{3})$.

The radius of gyration can be thought of as the ``effective radius'' of the mass distribution with respect to its inertial response to rotation (``gyration'') about the chosen axis.

Most cross-sectional shapes (e.g., rectangular), have at least two radii of gyration. A circular cross-section has only one, and its radius of gyration is equal to half its radius, as shown in the next section.

Circular Cross-Section

For a circular cross-section of radius $ a$, Eq.$ \,$(B.11) tells us that the squared radius of gyration about any line passing through the center of the cross-section is given by

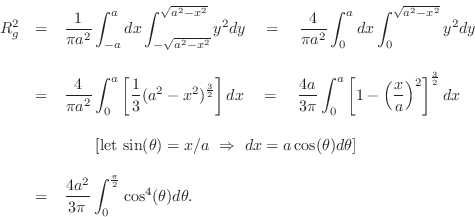
\begin{eqnarray*} R_g^2 &=& \frac{1}{\pi a^2} \int_{-a}^a dx \int_{-\sqrt{a^2-x^... ...frac{4a^2}{3\pi} \int_{0}^{\frac{\pi}{2}} \cos^4(\theta)d\theta. \end{eqnarray*}

Using the elementrary trig identity $ \cos(2\theta)=2\cos^2(\theta)-1$, we readily derive

$\displaystyle \cos^4(\theta) = \frac{1}{8}\cos(4\theta) + \frac{1}{2}\cos(2\theta) + \frac{3}{8}. $

The first two terms of this expression contribute zero to the integral from 0 to $ \pi /2$, while the last term contributes $ 3\pi/16$, yielding

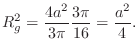
$\displaystyle R_g^2 = \frac{4a^2}{3\pi} \frac{3\pi}{16} = \frac{a^2}{4}. $

Thus, the radius of gyration about any midline of a circular cross-section of radius $ a$ is

$\displaystyle R_g = \frac{a}{2}. $

For a circular tube in which the mass of the cross-section lies within a circular annulus having inner radius $ b$ and outer radius $ a$, the radius of gyration is given by

$\displaystyle R_g = \frac{\sqrt{a^2-b^2}}{2}. \protect$ (B.12)

Next Section:
Two Masses Connected by a Rod
Previous Section:
Area Moment of Inertia