DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Area Moment of Inertia

The area moment of inertia is the second moment of an area $ A$ around a given axis:

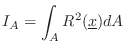
$\displaystyle I_A = \int_A R^2(\underline{x}) dA $

where $ dA$ denotes a differential element of the area (summing to $ A$), and $ R(\underline{x})$ denotes its distance from the axis of rotation.

Comparing with the definition of mass moment of inertia in §B.4.4 above, we see that mass is replaced by area in the area moment of inertia.

In a planar mass distribution with total mass $ M$ uniformly distributed over an area $ A$ (i.e., a constant mass density of $ \rho=M/A$), the mass moment of inertia $ I_\rho$ is given by the area moment of inertia $ I_A$ times mass-density $ \rho$:

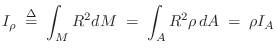
$\displaystyle I_\rho \isdefs \int_M R^2 dM \eqsp \int_A R^2 \rho\, dA \eqsp \rho I_A $

Next Section:
Radius of Gyration
Previous Section:
Stretch Rule