Relation to Stochastic Processes
Property.
If a stationary random process ![]() has a rational power spectral
density
has a rational power spectral
density
![]() corresponding to an autocorrelation function
corresponding to an autocorrelation function
![]() , then
, then
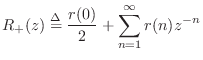
Proof.
By the representation theorem [19, pp. 98-103] there exists
an asymptotically stable filter
![]() which will produce a
realization of
which will produce a
realization of ![]() when driven by white noise, and we have
when driven by white noise, and we have
![]() . We define the analytic continuation
of
. We define the analytic continuation
of
![]() by
by
![]() . Decomposing
. Decomposing ![]() into a sum of
causal and anti-causal components gives
into a sum of
causal and anti-causal components gives

where ![]() is found by equating coefficients of like powers of
is found by equating coefficients of like powers of ![]() in
in
Since the poles of ![]() and
and ![]() are the same,
it only remains to be shown that
re
are the same,
it only remains to be shown that
re![]() .
.
Since spectral power is nonnegative,
![]() for all
for all ![]() , and so
, and so
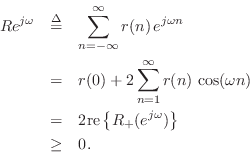
![]()
Next Section:
Relation to Schur Functions
Previous Section:
Power-Complementary Reflection and Transmission




















