State-Space Analysis

Free Books Physical Audio Signal Processing

We will now use state-space analysis^C.15[449] to determine Equations (C.133-C.136).

From Equations (C.128-C.132),

$\displaystyle x_1(n+1) = c[g x_1(n) + x_2(n)] - x_2(n) = c\,g x_1(n) + (c-1) x_2(n)$

and

$\displaystyle x_2(n+1) = g x_1(n) + c[g x_1(n) + x_2(n)] = (1+c) g x_1(n) + c\,x_2(n)$

In matrix form, the state time-update can be written

$\displaystyle \left[\begin{array}{c} x_1(n+1) \\ [2pt] x_2(n+1) \end{array}\rig... ...bf{A} \left[\begin{array}{c} x_1(n) \\ [2pt] x_2(n) \end{array}\right] \protect$

(C.136)

or, in vector notation,

$\displaystyle \underline{x}(n+1)$	$\displaystyle =$	$\displaystyle \mathbf{A}\underline{x}(n) + \mathbf{B}u(n)$	(C.137)
$\displaystyle y(n)$	$\displaystyle =$	$\displaystyle \mathbf{C}\underline{x}(n)$	(C.138)

where we have introduced an input signal

, which sums into the state vector via the $2\times 1$ (or $2\times N_u$ ) vector $\mathbf{B}$ . The output signal is defined as the $1\times 2$ vector $\mathbf{C}$ times the state vector $\underline{x}(n)$ . Multiple outputs may be defined by choosing $\mathbf{C}$ to be an $N_y \times 2$ matrix.

A basic fact from linear algebra is that the determinant of a matrix is equal to the product of its eigenvalues. As a quick check, we find that the determinant of is

$\displaystyle \det{\mathbf{A}} = c^2g - g(c+1)(c-1) = c^2g - g(c^2-1) = c^2g - gc^2+g = g. \protect$

(C.139)

When the eigenvalues ${\lambda_i}$ of $\mathbf{A}$ (system poles) are complex, then they must form a complex conjugate pair (since $\mathbf{A}$ is real), and we have $\det{\mathbf{A}} = \vert{\lambda_i}\vert^2 = g$ . Therefore, the system is stable if and only if $\vert g\vert<1$ . When making a digital sinusoidal oscillator from the system impulse response, we have $\vert g\vert=1$ , and the system can be said to be ``marginally stable''. Since an undriven sinusoidal oscillator must not lose energy, and since every lossless state-space system has unit-modulus eigenvalues (consider the modal representation), we expect $\left\vert\det{A}\right\vert=1$ , which occurs for

Note that $\underline{x}(n) = \mathbf{A}^n\underline{x}(0)$ . If we diagonalize this system to obtain $\tilde{\mathbf{A}}= \mathbf{E}^{-1}\mathbf{A}\mathbf{E}$ , where $\tilde{\mathbf{A}}=$ diag $[\lambda_1,\lambda_2]$ , and $\mathbf{E}$ is the matrix of eigenvectors of $\mathbf{A}$ , then we have

$\displaystyle \tilde{\underline{x}}(n) = \tilde{A}^n\,\tilde{\underline{x}}(0) ... ...eft[\begin{array}{c} \tilde{x}_1(0) \\ [2pt] \tilde{x}_2(0) \end{array}\right]$

where $\tilde{\underline{x}}(n) \isdef \mathbf{E}^{-1}\underline{x}(n)$ denotes the state vector in these new ``modal coordinates''. Since $\tilde{A}$ is diagonal, the modes are decoupled, and we can write

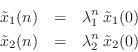
$\begin{eqnarray*} \tilde{x}_1(n) &=& \lambda_1^n\,\tilde{x}_1(0)\\ \tilde{x}_2(n) &=& \lambda_2^n\,\tilde{x}_2(0) \end{eqnarray*}$

If this system is to generate a real sampled sinusoid at radian frequency $\omega$ , the eigenvalues $\lambda_1$ and $\lambda_2$ must be of the form

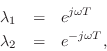
$\begin{eqnarray*} \lambda_1 &=& e^{j\omega T}\\ \lambda_2 &=& e^{-j\omega T}, \end{eqnarray*}$

(in either order) where $\omega$ is real, and denotes the sampling interval in seconds.

Thus, we can determine the frequency of oscillation $\omega$ (and verify that the system actually oscillates) by determining the eigenvalues $\lambda_i$ of . Note that, as a prerequisite, it will also be necessary to find two linearly independent eigenvectors of (columns of $\mathbf{E}$ ).