A Stiff Mass-Spring String Model
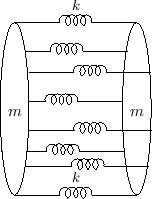
Following the classical derivation of the stiff-string wave equation [317,144], an obvious way to introduce stiffness in the mass-spring chain is to use a bundle of mass-spring chains to form a kind of ``lumped stranded cable''. One section of such a model is shown in Fig.9.27. Each mass is now modeled as a 2D mass disk. Complicated rotational dynamics can be avoided by assuming no torsional waves (no ``twisting'' motion) (§B.4.20).
A three-spring-per-mass model is shown in Fig.9.28
[266]. The spring positions alternate between angles
![]() , say, on one side of a mass disk and
, say, on one side of a mass disk and
![]() on the other side in order to provide effectively
six spring-connection points around the mass disk for only
three connecting springs per section. This improves isotropy
of the string model with respect to bending direction.
on the other side in order to provide effectively
six spring-connection points around the mass disk for only
three connecting springs per section. This improves isotropy
of the string model with respect to bending direction.
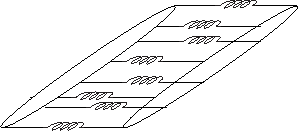
A problem with the simple mass-spring-chain-bundle is that there is no
resistance whatsoever to shear deformation, as is clear from
Fig.9.29. To rectify this problem (which does not
arise due implicit assumptions when classically deriving the
stiff-string wave equation), diagonal springs can be added to the
model, as shown in
Fig.![]() .
.
In the simulation results reported in [266], the spring-constants of the shear springs were chosen so that their stiffness in the longitudinal direction would equal that of the longitudinal springs.
Next Section:
Nonlinear Piano-String Equations of Motion in State-Space Form
Previous Section:
Checking the Approximations








![\includegraphics[width=0.8\twidth]{eps/masssprings3circ}](http://www.dsprelated.com/josimages_new/pasp/img2286.png)
![\includegraphics[width=0.4\twidth]{eps/masssprings3shear}](http://www.dsprelated.com/josimages_new/pasp/img2288.png)











