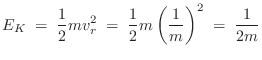Striking One of the Masses
Now let
![]() . That is, we apply an impulse
of vertical momentum to the mass on the right at time 0.
. That is, we apply an impulse
of vertical momentum to the mass on the right at time 0.
In this case, the unit of vertical momentum is transferred entirely to the mass on the right, so that
Note that the velocity of the center-of-mass ![]() is the
same as it was when we hit the midpoint of the rod. This is an
important general equivalence: The sum of all external force vectors
acting on a rigid body can be applied as a single resultant force
vector to the total mass concentrated at the center of mass to find
the linear (translational) motion produced. (Recall from §B.4.1
that such a sum is the same as the sum of all radially acting external
force components, since the tangential components contribute only to
rotation and not to translation.)
is the
same as it was when we hit the midpoint of the rod. This is an
important general equivalence: The sum of all external force vectors
acting on a rigid body can be applied as a single resultant force
vector to the total mass concentrated at the center of mass to find
the linear (translational) motion produced. (Recall from §B.4.1
that such a sum is the same as the sum of all radially acting external
force components, since the tangential components contribute only to
rotation and not to translation.)
All of the kinetic energy is in the mass on the right just after time zero:
However, after time zero, things get more complicated, because the mass on the left gets dragged into a rotation about the center of mass.
To simplify ongoing analysis, we can define a body-fixed frame
of referenceB.16 having its origin at the center of mass. Let ![]() denote a velocity in this frame. Since the velocity of the center of
mass is
denote a velocity in this frame. Since the velocity of the center of
mass is
![]() , we can convert any velocity
, we can convert any velocity ![]() in the
body-fixed frame to a velocity
in the
body-fixed frame to a velocity ![]() in the original frame by adding
in the original frame by adding
![]() to it, viz.,
to it, viz.,
In the body-fixed frame, all kinetic energy is rotational about
the origin. Recall (Eq.![]() (B.9)) that the moment of inertia for this
system, with respect to the center of mass at
(B.9)) that the moment of inertia for this
system, with respect to the center of mass at ![]() , is
, is
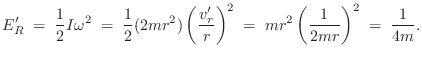
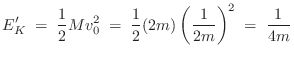
In summary, we defined a moving body-fixed frame having its origin at the center-of-mass, and the total kinetic energy was computed to be
It is important to note that, after time zero, both the linear
momentum of the center-of-mass (
![]() ), and the angular momentum in the body-fixed frame
(
), and the angular momentum in the body-fixed frame
(
![]() ) remain
constant over time.B.17 In the original space-fixed
frame, on the other hand, there is a complex transfer of momentum back
and forth between the masses after time zero.
) remain
constant over time.B.17 In the original space-fixed
frame, on the other hand, there is a complex transfer of momentum back
and forth between the masses after time zero.
Similarly, the translational kinetic energy of the total mass, treated as being concentrated at its center-of-mass, and the rotational kinetic energy in the body-fixed frame, are both constant after time zero, while in the space-fixed frame, kinetic energy transfers back and forth between the two masses. At all times, however, the total kinetic energy is the same in both formulations.
Next Section:
Cross-Product Magnitude
Previous Section:
Striking the Rod in the Middle