Free Books    Physical Audio Signal Processing  

Cross-Product Magnitude

It is a straightforward exercise to show that the cross-product magnitude is equal to the product of the vector lengths times the sine of the angle between them:B.21

$\displaystyle \left\Vert\,\underline{x}\times \underline{y}\,\right\Vert \eqsp ... ...dot\left\Vert\,\underline{y}\,\right\Vert \cdot \vert\sin(\theta)\vert \protect$ (B.16)

where

$\displaystyle \sin(\theta)\eqsp \sqrt{1-\cos^2(\theta)} $

with

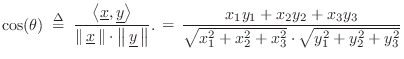
$\displaystyle \cos(\theta) \isdefs \frac{\left<\underline{x},\underline{y}\rig... ...c{x_1y_1+x_2y_2+x_3y_3}{\sqrt{x_1^2+x_2^2+x_3^2}\cdot\sqrt{y_1^2+y_2^2+y_3^2}} $

(Recall that the vector cosine of the angle between two vectors is given by their inner product divided by the product of their norms [451].)

To derive Eq.$ \,$(B.16), let's begin with the cross-product in matrix form as $ \underline{x}\times\underline{y}= \mathbf{X}\underline{y}$ using the first matrix form in the third line of the cross-product definition in Eq.$ \,$(B.15) above. Then

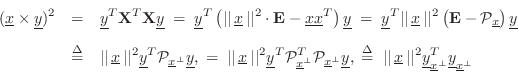
\begin{eqnarray*} (\underline{x}\times\underline{y})^2 &=& \underline{y}^T\mat... ...rline{x}^{\tiny\perp}}\underline{y}_{\underline{x}^{\tiny\perp}} \end{eqnarray*}

where $ \mathbf{E}=[\underline{e}_1,\underline{e}_2,\underline{e}_3]$ denotes the identity matrix in $ {\bf R}^3$, $ {\cal P}_{\underline{x}}$ denotes the orthogonal-projection matrix onto $ \underline{x}$ [451], $ {\cal P}_{\underline{x}}$ denotes the projection matrix onto the orthogonal complement of $ \underline{x}$, $ \underline{y}_{\underline{x}^{\tiny\perp}}$ denotes the component of $ \underline{y}$ orthogonal to $ \underline{x}$, and we used the fact that orthogonal projection matrices $ {\cal P}$ are idempotent (i.e., $ {\cal P}^2 ={\cal P}$) and symmetric (when real, as we have here) when we replaced $ {\cal P}_{\underline{x}^{\tiny\perp}}$ by $ {\cal P}^T_{\underline{x}^{\tiny\perp}}{\cal P}_{\underline{x}^{\tiny\perp}}$ above. Finally, note that the length of $ \underline{y}_{\underline{x}^{\tiny\perp}}$ is $ \vert\vert\,\underline{y}\,\vert\vert \cdot\vert\sin(\theta)\vert$, where $ \theta$ is the angle between the 1D subspaces spanned by $ \underline{x}$ and $ \underline{y}$ in the plane including both vectors. Thus,

$\displaystyle (\underline{x}\times\underline{y})^2 \eqsp \vert\vert\,\underline... ...line{x}\,\vert\vert ^2 \vert\vert\,\underline{y}\,\vert\vert ^2\sin^2(\theta), $

which establishes the desired result:

$\displaystyle \left\Vert\,\underline{x}\times\underline{y}\,\right\Vert = \vert... ...t\vert \cdot \vert\vert\,\underline{y}\,\vert\vert \cdot\vert\sin(\theta)\vert $

Moreover, this proof gives an appealing geometric interpretation of the vector cross-product $ \underline{x}\times\underline{y}$ as having magnitude given by the product of $ \vert\vert\,\underline{x}\,\vert\vert $ times the norm of the difference between $ \underline{x}$ and the orthogonal projection of $ \underline{x}$ onto $ \underline{y}$ ( $ \vert\vert\,\underline{x}\times\underline{y}\,\vert\vert = \vert\vert\,\underl... ... \vert\vert\,\underline{x}-{\cal P}_{\underline{y}}(\underline{x})\,\vert\vert $) or vice versa ( $ \vert\vert\,\underline{x}\times\underline{y}\,\vert\vert = \vert\vert\,\underl... ... \vert\vert\,\underline{y}-{\cal P}_{\underline{x}}(\underline{y})\,\vert\vert $). In this geometric picture it is clear that the cross-product magnitude is maximized when the vectors are orthogonal, and it is zero when the vectors are collinear. It is ``length times orthogonal length.''

The direction of the cross-product vector is then taken to be orthogonal to both $ \underline{x}$ and $ \underline{y}$ according to the right-hand rule. This orthogonality can be checked by verifying that $ \mathbf{X}\underline{x}=\mathbf{Y}\underline{y}=\underline{0}$. The right-hand-rule parity can be checked by rotating the space so that $ \underline{x}'=[ \vert\vert\,\underline{x}\,\vert\vert ,0,0]^T$ and $ \underline{y}'=[ \vert\vert\,\underline{y}\,\vert\vert \cos(\theta), \vert\vert\,\underline{y}\,\vert\vert \sin(\theta),0]^T$ in which case $ \underline{x}'\times\underline{y}' = \vert\vert\,\underline{x}\,\vert\vert [0,... ...}\,\vert\vert \vert\vert\,\underline{y}\,\vert\vert \sin(\theta)\underline{e}_3$. Thus, the cross product points ``up'' relative to the $ (\underline{x},\underline{y})$ plane for $ \theta \in(0,\pi)$ and ``down'' for $ \theta\in(0,-\pi)$.

Next Section:
Mass Moment of Inertia as a Cross Product
Previous Section:
Striking One of the Masses