In summary, we have characterized the mass on the string in terms of
its reflectance and transmittance from either string. For force
waves, we have outgoing waves given by
or
in terms of the incoming waves
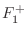
and
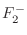
, the
force
reflectance

, and the force transmittance
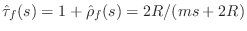
. We may say that the mass
creates a
dynamic scattering junction on the string. (If there
were no dependency on

, such as when a
dashpot is affixed to the
string, we would simply call it a
scattering junction.) The
above form of the dynamic scattering junction is analogous to the
Kelly-Lochbaum scattering junction (§
C.8.4).
The general relation
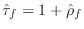
can be used to simplify the
Kelly-Lochbaum form to a
one-filter scattering junction
analogous to the
one-multiply scattering junction (§
C.8.5):
The one-filter form follows from the observation that
 appears in both computations, and therefore need only be implemented once:
appears in both computations, and therefore need only be implemented once:
This structure is diagrammed in Fig.9.20.
Figure 9.20:
Continuous-time force-wave simulation
diagram, in one-filter form, for an ideal string with a point mass
attached.
![\includegraphics[width=\twidth]{eps/massstringdwms}](http://www.dsprelated.com/josimages_new/pasp/img2153.png) |
Again, the above results follow immediately from the more general
formulation of §C.12.
Next Section: Digital Waveguide Mass-String ModelPrevious Section: Force Wave Mass-String Model

![$\displaystyle \left[\begin{array}{c} F^{+}_2 \\ [2pt] F^{-}_1 \end{array}\right...
...ay}\right] \left[\begin{array}{c} F^{+}_1 \\ [2pt] F^{-}_2 \end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2144.png)
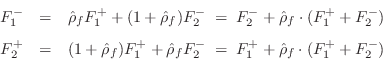
![]() appears in both computations, and therefore need only be implemented once:
appears in both computations, and therefore need only be implemented once:
![\begin{eqnarray*}
F^{+}&\isdef & \hat{\rho}_f\cdot(F^{+}_1+F^{-}_2)\\ [5pt]
F^{-}_1 &=& F^{-}_2 + F^{+}\\ [5pt]
F^{+}_2 &=& F^{+}_1 + F^{+}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2152.png)
![\includegraphics[width=\twidth]{eps/massstringdwms}](http://www.dsprelated.com/josimages_new/pasp/img2153.png)



















