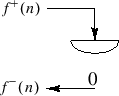Free Books
   Free Books    Physical Audio Signal Processing  

Wave Digital Dashpot

Starting with a dashpot with coefficient $ \mu $, we have

$\displaystyle R(s) = \mu $

and reflectance

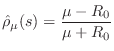
$\displaystyle \hat{\rho}_\mu(s) = \frac{\mu - R_0}{\mu + R_0} $

This time, choosing $ R_0$ equal to the element value gives

$\displaystyle \hat{\rho}_\mu(s) = 0 $

Conformally mapping the zero function yields the zero function so that

$\displaystyle \fbox{$\displaystyle \hat{\tilde{\rho}}_\mu(z) = 0$} $

as well. Thus, the WDF of a dashpot is a ``wave sink,'' as diagrammed in Fig.F.4.
Figure F.4: Wave flow diagram for the Wave Digital Dashpot.
\includegraphics{eps/lWaveDigitalDashpot}
In the context of waveguide theory, a zero reflectance corresponds to a matched impedance, i.e., the terminating transmission-line impedance equals the characteristic impedance of the line. The difference equation for the wave digital dashpot is simply $ f^{{-}}(n)=0$. While this may appear overly degenerate at first, remember that the interface to the element is a port at impedance $ R_0=\mu$. Thus, in this particular case only, the infinitesimal waveguide interface is the element itself.
Next Section:
Limiting Cases
Previous Section:
Wave Digital Spring