DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

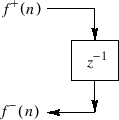
Wave Digital Spring

In the case of a spring with stiffness $ k$, we have the impedance

$\displaystyle R(s) = k/s $

which gives the reflectance

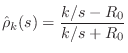
$\displaystyle \hat{\rho}_k(s) = \frac{k/s - R_0}{k/s + R_0} $

As before, we may eliminate $ k$ by choosing $ R_0=k$ to get

$\displaystyle \hat{\rho}_k(s) = \frac{1 - s }{1 + s} = z^{-1} $

under the bilinear transform. So we have the digital reflectance

$\displaystyle \fbox{$\displaystyle \hat{\tilde{\rho}}_k(z) = z^{-1}$} \qquad\makebox[0pt][l]{(Wave Digital Spring)} $

and corresponding difference equation

$\displaystyle f^{{-}}(n) = f^{{+}}(n-1). $

Again the delay-free path has been eliminated. The wave flow diagram is shown in Fig.F.3.

Figure F.3: Wave flow diagram for the Wave Digital Spring.
\includegraphics{eps/lWaveDigitalSpring}

Thus, the WDF of a spring is simply a unit-sample delay, which is just the negative of the WDF mass. If we were to switch to velocity waves instead of force waves, both masses and springs would again correspond to unit-sample delays, but the spring would become inverting and the mass non-inverting.

Next Section:
Wave Digital Dashpot
Previous Section:
Wave Digital Mass