Free Books
   Free Books    Physical Audio Signal Processing  

Wave Equation

The wave equation for the ideal vibrating string may be written as

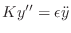$\displaystyle Ky''= \epsilon {\ddot y}$ (7.1)

where we define the following notation:

\begin{displaymath}\begin{array}{rclrcl} K& \isdef & \mbox{string tension} & \qq... ...isdef & \frac{\partial}{\partial x}y(t,x) \nonumber \end{array}\end{displaymath}    

As discussed in Chapter 1, the wave equation in this form can be interpreted as a statement of Newton's second law,

$\displaystyle \textit{force} = \textit{mass} \times \textit{acceleration}, $

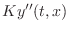
on a microscopic scale. Since we are concerned with transverse vibrations on the string, the relevant restoring force (per unit length) is given by the string tension (force along the string axis) times the curvature of the string, or $ Ky''(t,x)$; the restoring force is balanced at all times by the inertial force per unit length of the string which is equal to mass density (mass per unit length) times transverse acceleration, i.e., $ \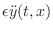epsilon {\ddot y}(t,x)$. See Appendix B for a review of basic physical concepts. The wave equation is derived in some detail in §B.6.

Next Section:
Wave Equation Applications
Previous Section:
Recent Research Modeling the Leslie