Wave Equation for the Vibrating String
Consider an elastic string under tension which is at rest along the
![]() dimension. Let
dimension. Let
![]() ,
,
![]() , and
, and
![]() denote the unit vectors in
the
denote the unit vectors in
the ![]() ,
, ![]() , and
, and ![]() directions, respectively. When a wave is
present, a point
directions, respectively. When a wave is
present, a point
![]() originally at
originally at ![]() along the string is
displaced to some point
along the string is
displaced to some point
![]() specified by the displacement
vector
specified by the displacement
vector
The displacement of a neighboring point originally at
![]() along the string can be specified as
along the string can be specified as
Let ![]() denote string tension along
denote string tension along ![]() when the string is at rest, and
when the string is at rest, and
![]() denote the vector tension at the point
denote the vector tension at the point
![]() in the present displaced
scenario under analysis. The net vector force acting on the infinitesimal
string element between points
in the present displaced
scenario under analysis. The net vector force acting on the infinitesimal
string element between points
![]() and
and
![]() is given by the vector sum of
the force
is given by the vector sum of
the force
![]() at
at
![]() and the force
and the force
![]() at
at
![]() , that is,
, that is,
![]() . If the string
has stiffness, the two forces will in general not be tangent to the string
at these points. The mass of the infinitesimal string element is
. If the string
has stiffness, the two forces will in general not be tangent to the string
at these points. The mass of the infinitesimal string element is
![]() ,
where
,
where ![]() denotes the mass per unit length of the string at rest. Applying
Newton's second law gives
denotes the mass per unit length of the string at rest. Applying
Newton's second law gives
where
The next step is to express the force
![]() in terms of the tension
in terms of the tension
![]() of the string at rest, the elastic constant of the string, and
geometrical factors. The displaced string element
of the string at rest, the elastic constant of the string, and
geometrical factors. The displaced string element
![]() is the
vector
is the
vector
having magnitude
Non-Stiff String
Let's now assume the string is perfectly flexible (zero stiffness) so
that the direction of the force vector
![]() is given by the unit
vector
is given by the unit
vector
![]() tangent to the string. (To accommodate
stiffness, it would be necessary to include a force component at right
angles to the string which depends on the curvature and stiffness of
the string.) The magnitude of
tangent to the string. (To accommodate
stiffness, it would be necessary to include a force component at right
angles to the string which depends on the curvature and stiffness of
the string.) The magnitude of
![]() at any position is the rest
tension
at any position is the rest
tension ![]() plus the incremental tension needed to stretch it the
fractional amount
plus the incremental tension needed to stretch it the
fractional amount
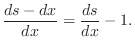
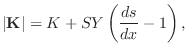
where no geometrical limitations have yet been placed on the magnitude of
The four equations (B.31) through (B.35) can be combined into a single vector wave equation that expresses the propagation of waves on the string having three displacement components. This differential equation is nonlinear, so that superposition no longer holds. Furthermore, the three displacement components of the wave are coupled together at all points along the string, so that the wave equation is no longer separable into three independent 1D wave equations.
To obtain a linear, separable wave equation, it is necessary to assume
that the strains
![]() ,
,
![]() , and
, and
![]() be
small compared with unity. This is the same assumption
(
be
small compared with unity. This is the same assumption
(
![]() ) necessary to derive the
usual wave equation for transverse vibrations only in the
) necessary to derive the
usual wave equation for transverse vibrations only in the ![]() -
-![]() plane.
plane.
When (B.35) is expanded into a Taylor series in the strains, and when only the first-order terms are retained, we obtain
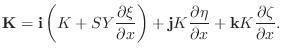 |
(B.36) |
This is the linearized wave equation for the string, based only on the assumptions of elasticity of the string, and strain magnitudes much less than unity. Using this linearized equation for the force
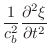 |
(B.37) | ||
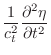 |
(B.38) | ||
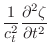 |
(B.39) |
where
In summary, the two transverse wave components and the longitudinal component may be considered independent (i.e., ``superposition'' holds with respect to vibrations in these three dimensions of vibration) provided powers higher than 1 of the strains (relative displacement) can be neglected, i.e.,
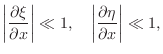 and
and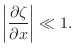
Wave Momentum
The physical forward momentum carried by a transverse wave along a string is conveyed by a secondary longitudinal wave [391].
A less simplified wave equation which
supports longitudinal wave momentum is given by [391, Eqns. 38ab]
| (B.40) | |||
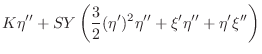 |
(B.41) | ||
| (B.42) |
where
| (B.43) | |||
| (B.44) |
(See also Eq.
Physically, the rising edge of a transverse wave generates a longitudinal displacement in the direction of wave travel that propagates ahead at a much higher speed (typically an order of magnitude faster). The falling edge of the transverse wave then cancels this forward displacement as it passes by. See [391] for further details (including computer simulations).
Next Section:
Properties of Gases
Previous Section:
Properties of Elastic Solids








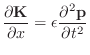
![$\displaystyle \left[\mathbf{i}\left(1+\frac{\partial \xi}{\partial x}\right)+
\...
...artial \eta}{\partial x} +
\mathbf{k}\frac{\partial \zeta}{\partial x}\right]dx$](http://www.dsprelated.com/josimages_new/pasp/img3011.png)
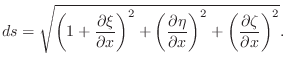
![$\displaystyle \mathbf{K}= \left[K+ SY\left(\frac{ds}{dx} - 1\right)\right]\frac{d{\bf s}}{ds}$](http://www.dsprelated.com/josimages_new/pasp/img3016.png)











