DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Wave Velocity

Because $ e^{st}$ is an eigenfunction under differentiation (i.e., the exponential function is its own derivative), it is often profitable to replace it with a generalized exponential function, with maximum degrees of freedom in its parametrization, to see if parameters can be found to fulfill the constraints imposed by differential equations.

In the case of the one-dimensional ideal wave equation (Eq.$ \,$(C.1)), with no boundary conditions, an appropriate choice of eigensolution is

$\displaystyle y(t,x) = e^{st+vx}$ (C.12)

Substituting into the wave equation yields

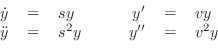
\begin{displaymath} \begin{array}{rclcrcl} {\dot y}& \,\mathrel{\mathop=}\,& sy... ...\quad & y''& \,\mathrel{\mathop=}\,& v^2y \nonumber \end{array}\end{displaymath}

Defining the wave velocity (or phase velocityC.2) as $ c \isdeftext {s/v}$, the wave equation becomes
$\displaystyle Kv^2y$ $\displaystyle =$ $\displaystyle \epsilon s^2y$ (C.13)
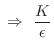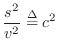$\displaystyle \,\,\Rightarrow\,\,\frac{K}{\epsilon }$ $\displaystyle =$ $\displaystyle \frac{s^2}{v^2} \isdef c^2$  
$\displaystyle \,\,\Rightarrow\,\,v$ $\displaystyle =$ $\displaystyle \pm \frac{s}{c}.$  

Thus

$\displaystyle y(t,x) = e^{s(t\pm x/c)} $

is a solution for all $ s$. By superposition,

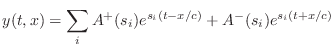
$\displaystyle y(t,x) = \sum\limits_i^{} A^{+}(s_i) e^{s_i(t-x/c)}+ A^{-}(s_i) e^{s_i(t+x/c)} $

is also a solution, where $ A^{+}(s_i)$ and $ A^{-}(s_i)$ are arbitrary complex-valued functions of arbitrary points $ s_i$ in the complex plane.

Next Section:
D'Alembert Derived
Previous Section:
String Slope from Velocity Waves