DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Zita-Rev1 Delay-Line Filters

In zita-rev1, the damping filter for each delay line consists of a low-shelf filter $ H_l(z)$ [449],4.19in series with a unique first-order lowpass filter $ H_h(z)$ that sets the high-frequency $ t_{60}$ to be half that of the middle-band at a particular frequency $ f_h$ (specified as ``HF Damping'' in the GUI). Since the filter $ H_h$ is constrained to be a lowpass, $ t_{60}(f)<t_{60}(f_h)$ for $ f>f_h$, i.e., the decay time gets shorter at higher frequencies.

Viewing the resulting damping filter $ H_d(z)=H_l(z)H_h(z)$ as a three-band filter bank (§3.7.5), let $ g_0$ and $ g_m$ denote the desired band gains at dc and ``middle frequencies'', respectively.4.20 Then the low shelf may be set for a desired dc-gain of $ g_0/g_m$, and its input (or output) signal multiplied by $ g_m$ to obtain the resulting filter

$\displaystyle H_l(z) \eqsp g_m + (g_0-g_m)\frac{1-p_l}{2}\frac{1+z^{-1}}{1-p_lz^{-1}}, $

where $ p_l$ denotes the (real) first-order lowpass pole, given by [449]

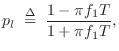
$\displaystyle p_l \isdefs \frac{1-\pi f_1T}{1+\pi f_1T}, $

where $ f_1$ specifies (in Hz) the crossover point between ``low'' and ``middle'' frequencies, and $ T$ denotes the sampling interval as usual.

The lowpass filter $ H_h(z)$ is also first order, and to provide half the middle-band $ t_{60}$ at the beginning of the ``high'' band, the lowpass should ``break'' to a gain of $ g_m$ at the ``HF Damping'' frequency $ f_h$ specified in the GUI. A unity-dc-gain one-pole lowpass has the form [449]

$\displaystyle H_h(z) = \frac{1-p_h}{1-p_hz^{-1}}, $

where the pole $ p_h$ must be found to give a gain of $ g_M$ at frequency $ f_h$:

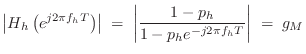
$\displaystyle \left\vert H_h\left(e^{j2\pi f_hT}\right)\right\vert \eqsp \left\vert\frac{1-p_h}{1-p_he^{-j2\pi f_hT}}\right\vert \eqsp g_M $

Squaring and normalizing yields a quadratic equation of the form $ p_h^2 + b\,p_h +1=0$. Solving for $ p_h$ using the quadratic formula yields

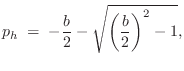
$\displaystyle p_h \eqsp -\frac{b}{2} - \sqrt{\left(\frac{b}{2}\right)^2 - 1}, $

where

$\displaystyle -\frac{b}{2} \eqsp \frac{1-g_M^2\cos(2\pi f_h T)}{1-g_M^2} > 1, $

and the unstable solution $ -b/2 + \sqrt{(b/2)^2 - 1} > 1$ is discarded. To ensure $ \vert g_M\vert<1$, the GUI must limit the middle-band $ t_{60}$ to finite values. (The upper limit is presently $ 8$ seconds for both low and middle frequencies.)

Next Section:
Spatialization of Reverberant Reflections
Previous Section:
Multiband Delay-Filter Design