Autocorrelation
The autocorrelation of a signal ![]() is simply the
cross-correlation of
is simply the
cross-correlation of ![]() with itself:
with itself:
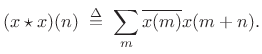 |
(3.24) |
From the correlation theorem, we have
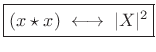
Note that this definition of autocorrelation is appropriate for signals having finite support (nonzero over a finite number of samples). For infinite-energy (but finite-power) signals, such as stationary noise processes, we define the sample autocorrelation to include a normalization suitable for this case (see Chapter 6 and Appendix C).
From the autocorrelation theorem we have that a digital-filter
impulse-response ![]() is that of a lossless allpass filter
[263] if and only if
is that of a lossless allpass filter
[263] if and only if
![]() .
In other words, the autocorrelation of the impulse-response of every
allpass filter is impulsive.
.
In other words, the autocorrelation of the impulse-response of every
allpass filter is impulsive.
Next Section:
Power Theorem for the DTFT
Previous Section:
Correlation Theorem for the DTFT



















