DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Beginning Statistical Signal Processing

The subject of statistical signal processing requires a background in probability theory, random variables, and stochastic processes [201]. However, only a small subset of these topics is really necessary to carry out practical spectrum analysis of noise-like signals (Chapter 6) and to fit deterministic models to noisy data. For a full textbook devoted to statistical signal processing, see, e.g., [121,95]. In this appendix, we will provide definitions for some of the most commonly encountered terms.

Random Variables & Stochastic Processes

For a full treatment of random variables and stochastic processes (sequences of random variables), see, e.g., [201]. For practical every-day signal analysis, the simplified definitions and examples below will suffice for our purposes.

Probability Distribution


Definition: A probability distribution $ \hat{p}(x)$ may be defined as a non-negative real function of all possible outcomes of some random event. The sum of the probabilities of all possible outcomes is defined as 1, and probabilities can never be negative.


Example: A coin toss has two outcomes, ``heads'' (H) or ``tails'' (T), which are equally likely if the coin is ``fair''. In this case, the probability distribution is

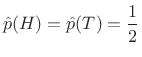$\displaystyle \hat{p}(H) = \hat{p}(T) = \frac{1}{2}$ (C.1)

where $ \hat{p}(x)$ denotes the probability of outcome $ x$ . That is, the total ``probability mass'' is divided equally between the two possible outcomes heads or tails. This is an example of a discrete probability distribution because all probability is assigned to two discrete points, as opposed to some continuum of possibilities.

Independent Events

Two probabilistic events $ H_1$ and $ H_2$ are said to be independent if the probability of $ H_1$ and $ H_2$ occurring together equals the product of the probabilities of $ H_1$ and $ H_2$ individually, i.e.,

$\displaystyle \hat{p}(H_1 H_2) = \hat{p}(H_1)(H_2)$ (C.2)

where $ \hat{p}(H_1 H_2)$ denotes the probability of $ H_1$ and $ H_2$ occurring together.


Example: Successive coin tosses are normally independent. Therefore, the probability of getting heads twice in a row is given by

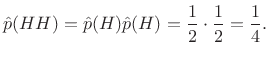$\displaystyle \hat{p}(H H) = \hat{p}(H)\hat{p}(H) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4}.$ (C.3)

Random Variable


Definition: A random variable $ x$ is defined as a real- or complex-valued function of some random event, and is fully characterized by its probability distribution.


Example: A random variable can be defined based on a coin toss by defining numerical values for heads and tails. For example, we may assign 0 to tails and 1 to heads. The probability distribution for this random variable is then

$\displaystyle \hat{p}(x) = \left\{\begin{array}{ll} \frac{1}{2}, & x = 0 \\ [5pt] \frac{1}{2}, & x = 1 \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right. \protect$ (C.4)


Example: A die can be used to generate integer-valued random variables between 1 and 6. Rolling the die provides an underlying random event. The probability distribution of a fair die is the discrete uniform distribution between 1 and 6. I.e.,

$\displaystyle \hat{p}(x) = \left\{\begin{array}{ll} \frac{1}{6}, & x = 1,2,\ldots,6 \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right.$ (C.5)


Example: A pair of dice can be used to generate integer-valued random variables between 2 and 12. Rolling the dice provides an underlying random event. The probability distribution of two fair dice is given by

$\displaystyle \hat{p}(x) = \left\{\begin{array}{ll} \frac{x-1}{36}, & x = 2,3,\ldots,7 \\ [5pt] \frac{13-x}{36}, & x = 7,8,\ldots,12 \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right.$ (C.6)

This may be called a discrete triangular distribution. It can be shown to be given by the convolution of the discrete uniform distribution for one die with itself. This is a general fact for sums of random variables (the distribution of the sum equals the convolution of the component distributions).


Example: Consider a random experiment in which a sewing needle is dropped onto the ground from a high altitude. For each such event, the angle of the needle with respect to north is measured. A reasonable model for the distribution of angles (neglecting the earth's magnetic field) is the continuous uniform distribution on $ [0,2\pi)$ , i.e., for any real numbers $ a$ and $ b$ in the interval $ [0,2\pi)$ , with $ a\leq b$ , the probability of the needle angle falling within that interval is

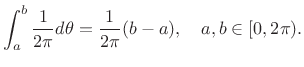$\displaystyle \int_a^b \frac{1}{2\pi}d\theta = \frac{1}{2\pi}(b-a), \quad a,b\in[0,2\pi).$ (C.7)

Note, however, that the probability of any single angle $ \theta$ is zero. This is our first example of a continuous probability distribution. Therefore, we cannot simply define the probability of outcome $ \theta$ for each $ \theta\in [0,2\pi)$ . Instead, we must define the probability density function (PDF):

$\displaystyle p(\theta) = \left\{\begin{array}{ll} \frac{1}{2\pi}, & 0\leq \theta < 2\pi \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right.$ (C.8)

To calculate a probability, the PDF must be integrated over one or more intervals. As follows from Lebesgue integration theory (``measure theory''), the probability of any countably infinite set of discrete points is zero when the PDF is finite. This is because such a set of points is a ``set of measure zero'' under integration. Note that we write $ \hat{p}(x)$ for discrete probability distributions and $ p(x)$ for PDFs. A discrete probability distribution such as that in (C.4) can be written as

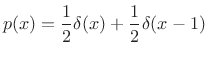$\displaystyle p(x) = \frac{1}{2}\delta(x) + \frac{1}{2}\delta(x-1)$ (C.9)

where $ \delta(x)$ denotes an impulse.C.1

Stochastic Process

(Again, for a more complete treatment, see [201] or the like.)


Definition: A stochastic process $ x$ is defined as a sequence of random variables $ x(n)$ , $ n=\ldots, -2,-1,0,1,2,\ldots\,$ .

A stochastic process may also be called a random process, noise process, or simply signal (when the context is understood to exclude deterministic components).

Stationary Stochastic Process


Definition: We define a stationary stochastic process $ x(n)$ , $ n=0,\pm1,\pm2,\ldots$ as a stochastic process consisting of identically distributed random variables $ x(n)$ . In particular, all statistical measures are time-invariant.

When a stochastic process is stationary, we may measure statistical features by averaging over time. Examples below include the sample mean and sample variance.

Expected Value


Definition: The expected value of a continuous random variable $ v\in(-\infty,\infty)$ is denoted $ E\{v\}$ and is defined by

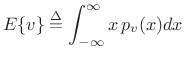$\displaystyle E\{v\} \isdef \int_{-\infty}^\infty x \, p_v(x) dx$ (C.12)

where $ p_v(x)$ denotes the probability density function (PDF) for the random variable v.


Example: Let the random variable $ v(n)$ be uniformly distributed between $ a$ and $ b$ , i.e.,

$\displaystyle p_v(x) = \left\{\begin{array}{ll} \frac{1}{b-a}, & a\leq x \leq b \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right.$ (C.13)

Then the expected value of $ v(n)$ is computed as

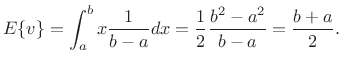$\displaystyle E\{v\} = \int_a^b x \frac{1}{b-a} dx = \frac{1}{2}\frac{b^2-a^2}{b-a} = \frac{b+a}{2}.$ (C.14)

Thus, the expected value of a random variable uniformly distributed between $ a$ and $ b$ is simply the average of $ a$ and $ b$ .

For a stochastic process, which is simply a sequence of random variables, $ E\{x(n)\}$ means the expected value of $ x(n)$ over ``all realizations'' of the random process $ x(\cdot)$ . This is also called an ensemble average. In other words, for each ``roll of the dice,'' we obtain an entire signal $ x(n),\, n=0,\pm1,\pm2,\cdots$ , and to compute $ E\{x(0)\}$ , say, we average together all of the values of $ x(0)$ obtained for all ``dice rolls.''

For a stationary random process $ x = \{x(n),\, n=0,\pm1,\pm2,\cdots\}$ , the random variables $ x(n)$ which make it up are identically distributed. As a result, we may normally compute expected values by averaging over time within a single realization of the random process, instead of having to average ``vertically'' at a single time instant over many realizations of the random process.C.2 Denote time averaging by

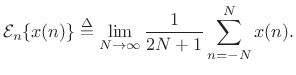$\displaystyle {\cal E}_n\{x(n)\} \isdef \lim_{N\to\infty}\frac{1}{2N+1}\sum_{n=-N}^N x(n).$ (C.15)

Then, for a stationary random processes, we have $ E\{x(n)\} = {\cal E}_n\{x(n)\}$ . That is, for stationary random signals, ensemble averages equal time averages.

We are concerned only with stationary stochastic processes in this book. While the statistics of noise-like signals must be allowed to evolve over time in high quality spectral models, we may require essentially time-invariant statistics within a single frame of data in the time domain. In practice, we choose our spectrum analysis window short enough to impose this. For audio work, 20 ms is a typical choice for a frequency-independent frame length.C.3 In a multiresolution system, in which the frame length can vary across frequency bands, several periods of the band center-frequency is a reasonable choice. As discussed in §5.5.2, the minimum number of periods required under the window for resolution of spectral peaks depends on the window type used.

Mean


Definition: The mean of a stochastic process $ v(n)$ at time $ n$ is defined as the expected value of $ v(n)$ :

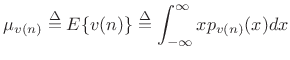$\displaystyle \mu_{v(n)} \isdef E\{v(n)\} \isdef \int_{-\infty}^\infty x p_{v(n)}(x) dx$ (C.16)

where $ p_{v(n)}(x)$ is the probability density function for the random variable $ v(n)$ .

For a stationary stochastic process $ v$ , the mean is given by the expected value of $ v(n)$ for any $ n$ . I.e., $ \mu_v = E\{v(n)\}$ for all $ n$ .

Sample Mean


Definition: The sample mean of a set of $ N$ samples from a particular realization of a stationary stochastic process $ v$ is defined as the average of those samples:

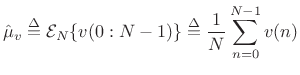$\displaystyle \hat{\mu}_{v} \isdef {\cal E}_N\{v(0:N-1)\} \isdef \frac{1}{N}\sum_{n=0}^{N-1} v(n)$ (C.17)

For a stationary stochastic process $ v$ , the sample mean is an unbiased estimator of the mean, i.e.,

$\displaystyle E\{\hat{\mu}_{v}\} = \mu_v.$ (C.18)

Variance


Definition: The variance or second central moment of a stochastic process $ v(n)$ at time $ n$ is defined as the expected value of $ \left\vert v(n)-\mu_{v(n)}\right\vert^2$ :

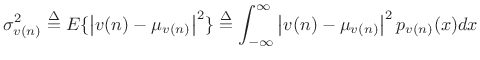$\displaystyle \sigma^2_{v(n)} \isdef E\{\left\vert v(n)-\mu_{v(n)}\right\vert^2\} \isdef \int_{-\infty}^\infty \left\vert v(n)-\mu_{v(n)}\right\vert^2 p_{v(n)}(x) dx$ (C.19)

where $ p_{v(n)}(x)$ is the probability density function for the random variable $ v(n)$ .

For a stationary stochastic process $ v$ , the variance is given by the expected value of $ \left\vert v(n)-\mu_v\right\vert^2$ for any $ n$ .

Sample Variance


Definition: The sample variance of a set of $ N$ samples from a particular realization of a stationary stochastic process $ v$ is defined as average squared magnitude after removing the known mean:

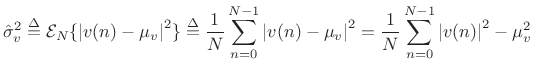$\displaystyle \hat{\sigma}^2_{v} \isdef {\cal E}_N\{\left\vert v(n)-\mu_v\right\vert^2\} \isdef \frac{1}{N}\sum_{n=0}^{N-1} \left\vert v(n)-\mu_v\right\vert^2 = \frac{1}{N}\sum_{n=0}^{N-1} \left\vert v(n)\right\vert^2 -\mu_v^2$ (C.20)

The sample variance is a unbiased estimator of the true variance when the mean is known, i.e.,

$\displaystyle E\{\hat{\sigma}^2_{v}\} = \sigma^2_v.$ (C.21)

This is easy to show by taking the expected value:
$\displaystyle E\{\hat{\sigma}^2_{v}\}$ $\displaystyle =$ $\displaystyle E{\cal E}_N\{\left\vert v(n)-\mu_v\right\vert^2\} = {\cal E}_N\{E\left\vert v(n)-\mu_v\right\vert^2\}$  
  $\displaystyle =$ $\displaystyle {\cal E}_N\{E\left\vert v(n)\right\vert^2-E\overline{v(n)}\mu_v-Ev(n)\overline{\mu_v}+\left\vert\mu_v\right\vert^2\}$  
  $\displaystyle =$ $\displaystyle {\cal E}_N\{\sigma_v^2+\left\vert\mu_v\right\vert^2-\overline{\mu_v}\mu_v-\mu_v\overline{\mu_v}+\left\vert\mu_v\right\vert^2\}$  
  $\displaystyle =$ $\displaystyle {\cal E}_N\{\sigma_v^2\} = \sigma^2_v. \protect$ (C.22)

When the mean is unknown, the sample mean is used in its place:

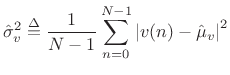$\displaystyle \hat{\sigma}^2_{v} \isdef \frac{1}{N-1}\sum_{n=0}^{N-1} \left\vert v(n)-\hat{\mu}_v\right\vert^2$ (C.23)

The normalization by $ N-1$ instead of $ N$ is necessary to make the sample variance be an unbiased estimator of the true variance. This adjustment is necessary because the sample mean is correlated with the term $ v(n)$ in the sample variance expression. This is revealed by replacing $ \mu_v$ with $ \hat{\mu}_v$ in the calculation of (C.22).

Correlation Analysis

Correlation analysis applies only to stationary stochastic processes (§C.1.5).

Cross-Correlation


Definition: The cross-correlation of two signals $ x$ and $ y$ may be defined by

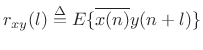$\displaystyle r_{xy}(l) \isdef E\{\overline{x(n)}y(n+l)\}$ (C.24)

I.e., it is the expected value (§C.1.6) of the lagged products in random signals $ x$ and $ y$ .

Cross-Power Spectral Density

The DTFT of the cross-correlation is called the cross-power spectral density, or ``cross-spectral density,'' ``cross-power spectrum,'' or even simply ``cross-spectrum.''

Autocorrelation

The cross-correlation of a signal with itself gives the autocorrelation function of that signal:

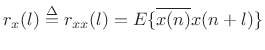$\displaystyle r_{x}(l) \isdef r_{xx}(l) = E\{\overline{x(n)}x(n+l)\}$ (C.25)

Note that the autocorrelation function is Hermitian:

$\displaystyle r_x(-l) = \overline{r_x(l)} $

When $ x$ is real, its autocorrelation is symmetric. More specifically, it is real and even.

Sample Autocorrelation

See §6.4.

Power Spectral Density

The Fourier transform of the autocorrelation function $ r_x(l)$ is called the power spectral density (PSD), or power spectrum, and may be denoted

$\displaystyle S_x(\omega) \isdef \hbox{\sc DTFT}_\omega(r_x). $

When the signal $ x$ is real, its PSD is real and even, like its autocorrelation function.

Sample Power Spectral Density

See §6.5.

White Noise


Definition: To say that $ v(n)$ is a white noise means merely that successive samples are uncorrelated:

$\displaystyle E\{v(n)v(n+m)\} = \left\{\begin{array}{ll} \sigma_v^2, & m=0 \\ [5pt] 0, & m\neq 0 \\ \end{array} \right. \isdef \sigma_v^2 \delta(m) \protect$ (C.26)

where $ E\{f(v)\}$ denotes the expected value of $ f(v)$ (a function of the random variables $ v(n)$ ).

In other words, the autocorrelation function of white noise is an impulse at lag 0. Since the power spectral density is the Fourier transform of the autocorrelation function, the PSD of white noise is a constant. Therefore, all frequency components are equally present--hence the name ``white'' in analogy with white light (which consists of all colors in equal amounts).

Making White Noise with Dice

An example of a digital white noise generator is the sum of a pair of dice minus 7. We must subtract 7 from the sum to make it zero mean. (A nonzero mean can be regarded as a deterministic component at dc, and is thus excluded from any pure noise signal for our purposes.) For each roll of the dice, a number between $ 1+1-7 = -5$ and $ 6+6-7=5$ is generated. The numbers are distributed binomially between $ -5$ and $ 5$ , but this has nothing to do with the whiteness of the number sequence generated by successive rolls of the dice. The value of a single die minus $ 3.5$ would also generate a white noise sequence, this time between $ -2.5$ and $ +2.5$ and distributed with equal probability over the six numbers

$\displaystyle \left[-\frac{5}{2}, -\frac{3}{2}, -\frac{1}{2}, \frac{1}{2}, \frac{3}{2}, \frac{5}{2}\right].$ (C.27)

To obtain a white noise sequence, all that matters is that the dice are sufficiently well shaken between rolls so that successive rolls produce independent random numbers.C.4

Independent Implies Uncorrelated

It can be shown that independent zero-mean random numbers are also uncorrelated, since, referring to (C.26),

$\displaystyle E\{\overline{v(n)}v(n+m)\} = \left\{\begin{array}{ll} E\{\left\vert v(n)\right\vert^2\} = \sigma_v^2, & m=0 \\ [5pt] E\{\overline{v(n)}\}\cdot E\{v(n+m)\}=0, & m\neq 0 \\ \end{array} \right. \isdef \sigma_v^2 \delta(m)$ (C.28)

For Gaussian distributed random numbers, being uncorrelated also implies independence [201]. For related discussion illustrations, see §6.3.

Estimator Variance

As mentioned in §6.12, the pwelch function in Matlab and Octave offer ``confidence intervals'' for an estimated power spectral density (PSD). A confidence interval encloses the true value with probability $ P$ (the confidence level). For example, if $ P=0.99$ , then the confidence level is $ 99\%$ .

This section gives a first discussion of ``estimator variance,'' particularly the variance of sample means and sample variances for stationary stochastic processes.

Sample-Mean Variance

The simplest case to study first is the sample mean:

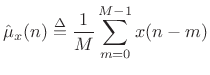$\displaystyle \hat{\mu}_x(n) \isdef \frac{1}{M}\sum_{m=0}^{M-1}x(n-m)$ (C.29)

Here we have defined the sample mean at time $ n$ as the average of the $ M$ successive samples up to time $ n$ --a ``running average''. The true mean is assumed to be the average over any infinite number of samples such as

$\displaystyle \mu_x = \lim_{M\to\infty}\hat{\mu}_x(n)$ (C.30)

or

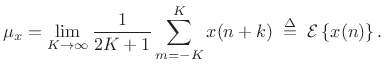$\displaystyle \mu_x = \lim_{K\to\infty}\frac{1}{2K+1}\sum_{m=-K}^{K}x(n+k) \isdefs {\cal E}\left\{x(n)\right\}.$ (C.31)

Now assume $ \mu_x=0$ , and let $ \sigma_x^2$ denote the variance of the process $ x(\cdot)$ , i.e.,

Var$\displaystyle \left\{x(n)\right\} \isdefs {\cal E}\left\{[x(n)-\mu_x]^2\right\} \eqsp {\cal E}\left\{x^2(n)\right\} \eqsp \sigma_x^2$ (C.32)

Then the variance of our sample-mean estimator $ \hat{\mu}_x(n)$ can be calculated as follows:

\begin{eqnarray*} \mbox{Var}\left\{\hat{\mu}_x(n)\right\} &\isdef & {\cal E}\left\{\left[\hat{\mu}_x(n)-\mu_x \right]^2\right\} \eqsp {\cal E}\left\{\hat{\mu}_x^2(n)\right\}\\ &=&{\cal E}\left\{\frac{1}{M}\sum_{m_1=0}^{M-1} x(n-m_1)\, \frac{1}{M}\sum_{m_2=0}^{M-1} x(n-m_2)\right\}\\ &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} {\cal E}\left\{x(n-m_1) x(n-m_2)\right\}\\ &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} r_x(\vert m_1-m_2\vert) \end{eqnarray*}

where we used the fact that the time-averaging operator $ {\cal E}\left\{\right\}$ is linear, and $ r_x(l)$ denotes the unbiased autocorrelation of $ x(n)$ . If $ x(n)$ is white noise, then $ r_x(\vert m_1-m_2\vert) = \sigma_x^2\delta(m_1-m_2)$ , and we obtain

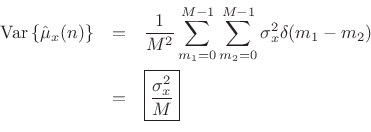
\begin{eqnarray*}\mbox{Var}\left\{\hat{\mu}_x(n)\right\} &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} \sigma_x^2\delta(m_1-m_2)\\ &=&\zbox {\frac{\sigma_x^2}{M}}\\ \end{eqnarray*}

We have derived that the variance of the $ M$ -sample running average of a white-noise sequence $ x(n)$ is given by $ \sigma_x^2/M$ , where $ \sigma_x^2$ denotes the variance of $ x(n)$ . We found that the variance is inversely proportional to the number of samples used to form the estimate. This is how averaging reduces variance in general: When averaging $ M$ independent (or merely uncorrelated) random variables, the variance of the average is proportional to the variance of each individual random variable divided by $ M$ .

Sample-Variance Variance

Consider now the sample variance estimator

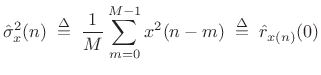$\displaystyle \hat{\sigma}_x^2(n) \isdefs \frac{1}{M}\sum_{m=0}^{M-1}x^2(n-m) \isdefs \hat{r}_{x(n)}(0)$ (C.33)

where the mean is assumed to be $ \mu_x ={\cal E}\left\{x(n)\right\}=0$ , and $ \hat{r}_{x(n)}(l)$ denotes the unbiased sample autocorrelation of $ x$ based on the $ M$ samples leading up to and including time $ n$ . Since $ \hat{r}_{x(n)}(0)$ is unbiased, $ {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} = {\cal E}\left\{\hat{r}_{x(n)}^2(0)\right\} = \sigma_x^2$ . The variance of this estimator is then given by

\begin{eqnarray*} \mbox{Var}\left\{\hat{\sigma}_x^2(n)\right\} &\isdef & {\cal E}\left\{[\hat{\sigma}_x^2(n)-\sigma_x^2]^2\right\}\\ &=& {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2-\sigma_x^4\right\} \end{eqnarray*}

where

\begin{eqnarray*} {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} &=& \frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}{\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\}\\ &=& \frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}r_{x^2}(\vert m_1-m_2\vert) \end{eqnarray*}

The autocorrelation of $ x^2(n)$ need not be simply related to that of $ x(n)$ . However, when $ x$ is assumed to be Gaussian white noise, simple relations do exist. For example, when $ m_1\ne m_2$ ,

$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = {\cal E}\left\{x^2(n-m_1)\right\}{\cal E}\left\{x^2(n-m_2)\right\}=\sigma_x^2\sigma_x^2= \sigma_x^4.$ (C.34)

by the independence of $ x(n-m_1)$ and $ x(n-m_2)$ , and when $ m_1=m_2$ , the fourth moment is given by $ {\cal E}\left\{x^4(n)\right\} = 3\sigma_x^4$ . More generally, we can simply label the $ k$ th moment of $ x(n)$ as $ \mu_k = {\cal E}\left\{x^k(n)\right\}$ , where $ k=1$ corresponds to the mean, $ k=2$ corresponds to the variance (when the mean is zero), etc.

When $ x(n)$ is assumed to be Gaussian white noise, we have

$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = \left\{\begin{array}{ll} \sigma_x^4, & m_1\ne m_2 \\ [5pt] 3\sigma_x^4, & m_1=m_2 \\ \end{array} \right.$ (C.35)

so that the variance of our estimator for the variance of Gaussian white noise is

Var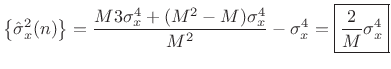$\displaystyle \left\{\hat{\sigma}_x^2(n)\right\} = \frac{M3\sigma_x^4 + (M^2-M)\sigma_x^4}{M^2} - \sigma_x^4 = \zbox {\frac{2}{M}\sigma_x^4}$ (C.36)

Again we see that the variance of the estimator declines as $ 1/M$ .

The same basic analysis as above can be used to estimate the variance of the sample autocorrelation estimates for each lag, and/or the variance of the power spectral density estimate at each frequency.

As mentioned above, to obtain a grounding in statistical signal processing, see references such as [201,121,95].

Next Section:
Gaussian Function Properties
Previous Section:
Selected Continuous Fourier Theorems