DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Correlation Theorem for the DTFT

We define the correlation of discrete-time signals $ x$ and $ y$ by

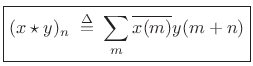
$\displaystyle \zbox {(x\star y)_n \isdefs \sum_m \overline{x(m)} y(m+n)} $

The correlation theorem for DTFTs is then

$\displaystyle \zbox {x\star y \;\longleftrightarrow\;\overline{X}\cdot Y} $


Proof:

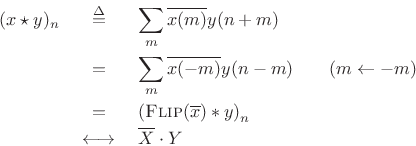
\begin{eqnarray*} (x\star y)_n &\isdef & \sum_m \overline{x(m)}y(n+m) \\ &=& \sum_m \overline{x(-m)}y(n-m) \qquad (m\leftarrow -m)\\ &=& \left(\hbox{\sc Flip}(\overline{x})\ast y\right)_n \\ &\;\longleftrightarrow\;& \overline{X} \cdot Y \end{eqnarray*}

where the last step follows from the convolution theorem of §2.3.5 and the symmetry result $ \hbox{\sc Flip}(\overline{x}) \;\longleftrightarrow\; \overline{X}$ of §2.3.2.

Next Section:
Autocorrelation
Previous Section:
Convolution Theorem for the DTFT