When 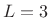 in (3.26), we obtain the Blackman family:
in (3.26), we obtain the Blackman family:
![$\displaystyle w_{B}(n)= w_R(n)\left[\alpha_0 + \alpha_1 \cos(\Omega_M n) + \alpha_2 \cos(2\Omega_M n)\right]$](http://www.dsprelated.com/josimages_new/sasp2/img407.png) |
(4.28) |
Relative to the generalized Hamming family (§
3.2), we
have added one more cosine weighted by
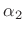
. We now therefore
have
three degrees of freedom to work with instead of two. In
the Hamming family, we used one degree of freedom to normalize the
window amplitude and the second was used either to maximize roll-off
rate (Hann) or
side-lobe rejection (Hamming). Now we can use two
remaining degrees of freedom (after normalization) to optimize these
objectives, or we can use one for each, resulting in three subtypes
within the Blackman window family.
Next Section: Classic BlackmanPrevious Section: The MLT Sine Window
![]() in (3.26), we obtain the Blackman family:
in (3.26), we obtain the Blackman family:
![]() in (3.26), we obtain the Blackman family:
in (3.26), we obtain the Blackman family: