Generalized Hamming Window Family

Free Books Spectral Audio Signal Processing

The generalized Hamming window family is constructed by multiplying a rectangular window by one period of a cosine. The benefit of the cosine tapering is lower side-lobes. The price for this benefit is that the main-lobe doubles in width. Two well known members of the generalized Hamming family are the Hann and Hamming windows, defined below.

The basic idea of the generalized Hamming family can be seen in the frequency-domain picture of Fig.3.8. The center dotted waveform is the aliased sinc function $0.5\cdot W_R(\omega) = 0.5\cdot M\cdot\hbox{asinc}_M(\omega)$ (scaled rectangular window transform). The other two dotted waveforms are scaled shifts of the same function, $0.25\cdot W_R(\omega\pm\Omega_M)$ . The sum of all three dotted waveforms gives the solid line. We see that

there is some cancellation of the side lobes, and
the width of the main lobe is doubled.

**Figure 3.8:** Construction of the generalized Hamming window transform as a superposition of three shifted aliased sinc functions.
$\includegraphics[width=3in]{eps/shiftedSincs}$

In terms of the rectangular window transform $W_R(\omega) = M\cdot\hbox{asinc}_M(\omega)$ (the zero-phase, unit-amplitude case), this can be written as

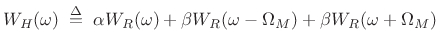$\displaystyle W_H( \omega ) \isdefs \alpha W_R( \omega ) + \beta W_R( \omega - \Omega_M ) + \beta W_R( \omega + \Omega_M )$

(4.15)

where $\alpha=1/2$ , $\beta=1/4$ in the example of Fig.3.8.

Using the shift theorem (§2.3.4), we can take the inverse transform of the above equation to obtain

$\displaystyle w_H = \alpha w_R(n) + \beta e^{-j\Omega_M n}w_R(n) + \beta e^{j \Omega_M n} w_R(n),$

(4.16)

or,

$\displaystyle \zbox {w_H(n) = w_R(n) \left[ \alpha + 2 \beta \cos \left( \frac{2 \pi n}{M} \right) \right].} \protect$

(4.17)

Choosing various parameters for $\alpha$ and $\beta$ result in different windows in the generalized Hamming family, some of which have names.

Hann or Hanning or Raised Cosine

The Hann window (or hanning or raised-cosine window) is defined based on the settings $\alpha=1/2$ and $\beta=1/4$ in (3.17):

$\displaystyle w_H(n)=w_R(n) \left[ \frac{1}{2} + \frac{1}{2} \cos( \Omega_M n) \right] = w_R(n) \cos^2\left(\frac{\Omega_M}{2} n\right) \protect$

(4.18)

where $\Omega_M \isdeftext 2\pi/M$ .

The Hann window and its transform appear in Fig.3.9. The Hann window can be seen as one period of a cosine ``raised'' so that its negative peaks just touch zero (hence the alternate name ``raised cosine''). Since it reaches zero at its endpoints with zero slope, the discontinuity leaving the window is in the second derivative, or the third term of its Taylor series expansion at an endpoint. As a result, the side lobes roll off approximately 18 dB per octave. In addition to the greatly accelerated roll-off rate, the first side lobe has dropped from dB (rectangular-window case) down to dB. The main-lobe width is of course double that of the rectangular window. For Fig.3.9, the window was computed in Matlab as hanning(21). Therefore, it is the variant that places the zero endpoints one-half sample to the left and right of the outermost window samples (see next section).

**Figure 3.9:** The Hann window (`hanning(21)`) and its DTFT.
$\includegraphics[width=4in]{eps/hanningWindow}$

Matlab for the Hann Window

In matlab, a length Hann window is designed by the statement

w = hanning(M);

which, in Matlab only is equivalent to

w = .5*(1 - cos(2*pi*(1:M)'/(M+1)));

For

, hanning(3) returns the following:

>> hanning(3)
ans =
     0.5
     1
     0.5

Note the curious use of M+1 in the denominator instead of M as we would expect from the family definition in (3.17). This perturbation serves to avoid using zero samples in the window itself. (Why bother to multiply explicitly by zero?) Thus, the Hann window as returned by Matlab hanning function reaches zero one sample beyond the endpoints to the left and right. The minus sign, which differs from (3.18), serves to make the window causal instead of zero phase.

The Matlab Signal Processing Toolbox also includes a hann function which is defined to include the zeros at the window endpoints. For example,

>> hann(3)
ans =
     0
     1
     0

This case is equivalent to the following matlab expression:

w = .5*(1 - cos(2*pi*(0:M-1)'/(M-1)));

The use of

is necessary to include zeros at both endpoints. The Matlab hann function is a special case of what Matlab calls ``generalized cosine windows'' (type gencoswin).

In Matlab, both hann(3,'periodic') and hanning(3,'periodic') produce the following window:

>> hann(3,'periodic')
ans =
     0
     0.75
     0.75

This case is equivalent to

w = .5*(1 - cos(2*pi*(0:M-1)'/M));

which agrees (finally) with definition (3.18). We see that in this case, the left zero endpoint is included in the window, while the one on the right lies one sample outside to the right. In general, the 'periodic' window option asks for a window that can be overlapped and added to itself at certain time displacements (

samples in this case) to produce a constant function. Use of ``periodic'' windows in this way is introduced in §7.3 and discussed more fully in Chapters 8 and 9.

In Octave, both the hann and hanning functions include the endpoint zeros.

In practical applications, it is safest to write your own window functions in the matlab language in order to ensure portability and consistency. After all, they are typically only one line of code!

In comparing window properties below, we will speak of the Hann window as having a main-lobe width equal to $4\Omega_M$ , and a side-lobe width $\Omega_M$ , even though in practice they may really be $4\Omega_{M\pm1}$ and $\Omega_{M\pm1}$ , respectively, as illustrated above. These remarks apply to all windows in the generalized Hamming family, as well as the Blackman-Harris family introduced in §3.3 below.

Summary of Hann window properties:

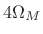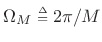
Main lobe is $4\Omega_M$ wide, $\Omega_M \isdeftext 2\pi/M$
First side lobe at -31dB
Side lobes roll off approximately 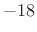dB per octave

Hamming Window

The Hamming window is determined by choosing $\alpha$ in (3.17) (with $\beta\isdeftext (1-\alpha)/2$ ) to cancel the largest side lobe [101].^4.4 Doing this results in the values

$\begin{eqnarray*} \alpha &=& \frac{25}{46} \approx 0.54\\ [5pt] \beta &=& \frac{1-\alpha}{2} \approx 0.23. \end{eqnarray*}$

The peak side-lobe level is approximately dB for the Hamming window [101].^4.5 It happens that this choice is very close to that which minimizes peak side-lobe level (down to dB--the lowest possible within the generalized Hamming family) [196]:

$\displaystyle \alpha = 0.53836\ldots$

(4.19)

Since rounding the optimal $\alpha$ to two significant digits gives

, the Hamming window can be considered the ``Chebyshev Generalized Hamming Window'' (approximately). Chebyshev-type designs normally exhibit equiripple error behavior, because the worst-case error (side-lobe level in this case) is minimized. However, within the generalized Hamming family, the asymptotic spectral roll-off is constrained to be at least

dB per octave due to the form (3.17) of all windows in the family. We'll discuss the true Chebyshev window in §3.10 below; we'll see that it is not monotonic from its midpoint to an endpoint, and that it is in fact impulsive at its endpoints. (To peek ahead at a Chebyshev window and transform, see Fig.3.31.) Generalized Hamming windows can have a step discontinuity at their endpoints, but no impulsive points.

**Figure 3.10:** A Hamming window and its transform.
$\includegraphics[width=\twidth]{eps/hammingWindow}$

The Hamming window and its DTFT magnitude are shown in Fig.3.10. Like the Hann window, the Hamming window is also one period of a raised cosine. However, the cosine is raised so high that its negative peaks are above zero, and the window has a discontinuity in amplitude at its endpoints (stepping discontinuously from 0.08 to 0). This makes the side-lobe roll-off rate very slow (asymptotically dB/octave). On the other hand, the worst-case side lobe plummets to dB,^4.6which is the purpose of the Hamming window. This is 10 dB better than the Hann case of Fig.3.9 and 28 dB better than the rectangular window. The main lobe is approximately $4\Omega_M$ wide, as is the case for all members of the generalized Hamming family ( $\beta\neq 0$ ).

Due to the step discontinuity at the window boundaries, we expect a spectral envelope which is an aliased version of a dB per octave (i.e., a $1/\omega$ roll-off is converted to a ``cosecant roll-off'' by aliasing, as derived in §3.1 and illustrated in Fig.3.6). However, for the Hamming window, the side-lobes nearest the main lobe have been strongly shaped by the optimization. As a result, the nearly dB per octave roll-off occurs only over an interior interval of the spectrum, well between the main lobe and half the sampling rate. This is easier to see for a larger , as shown in Fig.3.11, since then the optimized side-lobes nearest the main lobe occupy a smaller frequency interval about the main lobe.

**Figure 3.11:** A longer Hamming window and its transform.
$\includegraphics[width=\twidth]{eps/hammingWindowLong}$

Since the Hamming window side-lobe level is more than 40 dB down, it is often a good choice for ``1% accurate systems,'' such as 8-bit audio signal processing systems. This is because there is rarely any reason to require the window side lobes to lie far below the signal quantization noise floor. The Hamming window has been extensively used in telephone communications signal processing wherein 8-bit CODECs were standard for many decades (albeit $\mu$ -law encoded). For higher quality audio signal processing, higher quality windows may be required, particularly when those windows act as lowpass filters (as developed in Chapter 9).

Matlab for the Hamming Window

In matlab, a length Hamming window is designed by the statement

w = hamming(M);

which is equivalent to

w = .54 - .46*cos(2*pi*(0:M-1)'/(M-1));

Note that M-1 is used in the denominator rather than M+1 as in the Hann window case. Since the Hamming window cannot reach zero for any choice of samples of the defining raised cosine, it makes sense not to have M+1 here. Using M-1 (instead of M) provides that the returned window is symmetric, which is usually desired. However, we will learn later that there are times when M is really needed in the denominator (such as when the window is being used successively over time in an overlap-add scheme, in which case the sum of overlapping windows must be constant).

The hamming function in the Matlab Signal Processing Tool Box has an optional argument 'periodic' which effectively uses instead of . The default case is 'symmetric'. The following examples should help clarify the difference:

>> hamming(3) % same in Matlab and Octave
ans =
    0.0800
    1.0000
    0.0800
>> hamming(3,'symmetric') % Matlab only
ans =
    0.0800
    1.0000
    0.0800
>> hamming(3,'periodic') % Matlab only
ans =
    0.0800
    0.7700
    0.7700
>> hamming(4) % same in Matlab and Octave
ans =
    0.0800
    0.7700
    0.7700
    0.0800

Summary of Generalized Hamming Windows

Definition:

$\displaystyle w_H(n) = w_R(n) \left[ \alpha + 2 \beta \cos \left( \Omega_M n \right) \right], \quad n \in {\bf Z}, \; \Omega_M \isdef \frac{2 \pi}{M}$

(4.20)

where

$\displaystyle w_R(n) \isdefs \left\{\begin{array}{ll} 1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$

(4.21)

Transform:

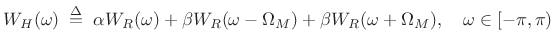$\displaystyle W_H( \omega ) \isdefs \alpha W_R( \omega ) + \beta W_R( \omega - \Omega_M ) + \beta W_R( \omega + \Omega_M ), \quad \omega\in[-\pi,\pi)$

(4.22)

where

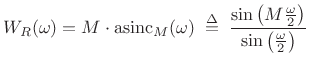$\displaystyle W_R(\omega) = M\cdot \hbox{asinc}_M(\omega) \isdefs \frac{\sin\left(M\frac{\omega}{2}\right)}{\sin\left(\frac{\omega}{2}\right)}$

(4.23)

Common Properties

Rectangular + scaled-cosine window
Cosine has one period across the window
Symmetric ( $\Rightarrow$ zero or linear phase)
Positive (by convention on $\alpha$ and $\beta$ )
Main lobe is 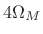$4\Omega_M$ radians per sample wide, where $\Omega_M\isdef 2\pi/M$
Zero-crossings (``notches'') in window transform at intervals of $\Omega_M$ outside of main lobe

Figure 3.12 compares the window transforms for the rectangular, Hann, and Hamming windows. Note how the Hann window has the fastest roll-off while the Hamming window is closest to being equal-ripple. The rectangular window has the narrowest main lobe.

**Figure 3.12:** Comparison of window transforms for the rectangular, Hann, and Hamming windows.
$\includegraphics[width=\twidth]{eps/RectHannHamm}$

Rectangular window properties:

Abrupt transition from 1 to 0 at the window endpoints
Roll-off is asymptotically 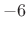dB per octave (as $T\rightarrow 0$ )
First side lobe is 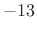dB relative to main-lobe peak

Hann window properties:

Smooth transition to zero at window endpoints
Roll-off is asymptotically -18 dB per octave
First side lobe is 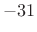dB relative to main-lobe peak

Hamming window properties:

Discontinuous ``slam to zero'' at endpoints
Roll-off is asymptotically -6 dB per octave
Side lobes are closer to ``equal ripple''
First side lobe is 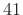dB down = 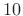dB better than Hann^4.7

The MLT Sine Window

The modulated lapped transform (MLT) [160] uses the sine window, defined by

$\displaystyle w(n) = \sin\left[\left(n+\frac{1}{2}\right)\frac{\pi}{2M}\right], \quad n=0,1,2,\ldots,2M-1\,.$

(4.24)

The sine window is used in MPEG-1, Layer 3 (MP3 format), MPEG-2 AAC, and MPEG-4 [200].

Properties:

Side lobes 24 dB down
Asymptotically optimal coding gain [159]
Zero-phase-window transform (``truncated cosine window'') has smallest moment of inertia over all windows [202]:

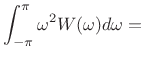$\displaystyle \int_{-\pi}^{\pi} \omega^2 W(\omega)d\omega =$ min (4.25)

Note that in perceptual audio coding systems, there is both an analysis window and a synthesis window. That is, the sine window is deployed twice, first when encoding the signal, and second when decoding. As a result, the sine window is squared in practical usage, rendering it equivalent to a Hann window ( $\cos^2$ ) in the final output signal (when there are no spectral modifications).

It is of great practical value that the second window application occurs after spectral modifications (such as spectral quantization); any distortions due to spectral modifications are tapered gracefully to zero by the synthesis window. Synthesis windows were introduced at least as early as 1980 [213,49], and they became practical for audio coding with the advent of time-domain aliasing cancellation (TDAC) [214]. The TDAC technique made it possible to use windows with 50% overlap without suffering a doubling of the number of samples in the short-time Fourier transform. TDAC was generalized to ``lapped orthogonal transforms'' (LOT) by Malvar [160]. The modulated lapped transform (MLT) is a variant of LOT used in conjunction with the modulated discrete cosine transform (MDCT) [160]. See also [287] and [291].

Next Section:
Blackman-Harris Window Family
Previous Section:
The Rectangular Window