Blackman-Harris Window Family
The Blackman-Harris (BH) window family is a straightforward generalization of the Hamming family introduced in §3.2. Recall from that discussion that the generalized Hamming family was constructed using a summation of three shifted and scaled aliased-sinc-functions (shown in Fig.3.8). The Blackman-Harris family is obtained by adding still more shifted sinc functions:
where
 , and
, and 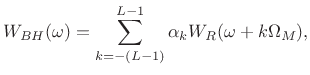 |
(4.27) |
where
Note that for ![]() , we obtain the rectangular window, and for
, we obtain the rectangular window, and for ![]() ,
the BH family specializes to the generalized Hamming family.
,
the BH family specializes to the generalized Hamming family.
Blackman Window Family
When ![]() in (3.26), we obtain the Blackman family:
in (3.26), we obtain the Blackman family:
| (4.28) |
Relative to the generalized Hamming family (§3.2), we have added one more cosine weighted by
Classic Blackman
The so-called ``Blackman Window'' is the specific case for which
![]()
![]() , and
, and
![]() . It has
the following properties:
. It has
the following properties:
- Side lobes roll off at about
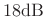 per octave (like Hann)
per octave (like Hann)
- Side-lobe level is about
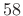 dB (worst case)
dB (worst case)
- One degree of freedom used to increase the roll-off rate from 6dB/octave (like rectangular) to 18 dB per octave by matching amplitude and slope to 0 at the window endpoints
- One degree of freedom is used to minimize side lobes (like Hamming)
- One degree of freedom is used to scale the window
Matlab for the Classic Blackman Window
N = 101; L = 3; No2 = (N-1)/2; n=-No2:No2; ws = zeros(L,3*N); z = zeros(1,N); for l=0:L-1 ws(l+1,:) = [z,cos(l*2*pi*n/N),z]; end alpha = [0.42,0.5,0.08]; % Classic Blackman w = alpha * ws;
Figure 3.13 plots the classic Blackman Window and its transform.
Three-Term Blackman-Harris Window
The classic Blackman window of the previous section is a three-term
window in the Blackman-Harris family (![]() ), in which one degree of
freedom is used to minimize side-lobe level, and the other is used to
maximize roll-off rate. Harris [101, p. 64] defines the
three-term
Blackman-Harris window as the one which uses both degrees of
freedom to minimize side-lobe level. An improved design is given in
Nuttall [196, p. 89], and its properties are as follows:
), in which one degree of
freedom is used to minimize side-lobe level, and the other is used to
maximize roll-off rate. Harris [101, p. 64] defines the
three-term
Blackman-Harris window as the one which uses both degrees of
freedom to minimize side-lobe level. An improved design is given in
Nuttall [196, p. 89], and its properties are as follows:
-
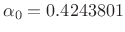
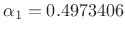 , and
, and
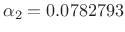 .
.
- Side-lobe level
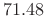 dB
dB
- Side lobes roll off
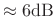 per octave in the absence of aliasing
(like rectangular and Hamming)
per octave in the absence of aliasing
(like rectangular and Hamming)
- All degrees of freedom (scaling aside) are used to minimize side lobes (like Hamming)
Figure 3.14 plots the three-term Blackman-Harris Window and its transform. Figure 3.15 shows the same display for a much longer window of the same type, to illustrate its similarity to the rectangular window (and Hamming window) at high frequencies.
Frequency-Domain Implementation of the
Blackman-Harris Family
The Blackman-Harris window family can be very efficiently implemented
in the frequency domain as a ![]() -point convolution with the
spectrum of the unwindowed data.
-point convolution with the
spectrum of the unwindowed data.
For example, to implement a zero-phase Hann window,
- Start with a length
 rectangular window
rectangular window
- Take an
 -point DFT
-point DFT
- Convolve the DFT data with the 3-point smoother
![$ W=[1/4,1/2,1/4]$](http://www.dsprelated.com/josimages_new/sasp2/img423.png)
Similarly, any Blackman window may be implemented as a 5-point
smoother in the frequency domain. More generally, any ![]() -term
Blackman-Harris window requires convolution of the critically sampled
spectrum with a smoother of length
-term
Blackman-Harris window requires convolution of the critically sampled
spectrum with a smoother of length ![]() .
.
Power-of-Cosine Window Family
Definition:
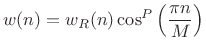 |
(4.29) |
where
Properties:
- The first
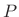 terms of the window's Taylor expansion, evaluated at the endpoints are identically 0
.
terms of the window's Taylor expansion, evaluated at the endpoints are identically 0
.
- Roll-off rate
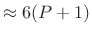 dB/octave.
dB/octave.
Special Cases:
-
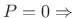 Rectangular window
Rectangular window
-
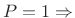 MLT sine window
MLT sine window
-
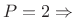 Hann window (``raised cosine'' = ``
Hann window (``raised cosine'' = ``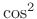 '')
'')
-
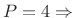 Alternative Blackman (maximized roll-off rate)
Alternative Blackman (maximized roll-off rate)
Thus, ![]() windows parametrize
windows parametrize ![]() -term Blackman-Harris windows
(for
-term Blackman-Harris windows
(for ![]() ) which are configured to use all degrees-of-freedom to
maximize roll-off rate.
) which are configured to use all degrees-of-freedom to
maximize roll-off rate.
Next Section:
Spectrum Analysis of an Oboe Tone
Previous Section:
Generalized Hamming Window Family








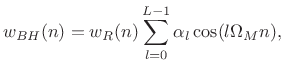
![\includegraphics[width=\twidth]{eps/blackmanWindow}](http://www.dsprelated.com/josimages_new/sasp2/img414.png)
![\includegraphics[width=\twidth]{eps/blackmanHarris3}](http://www.dsprelated.com/josimages_new/sasp2/img420.png)
![\includegraphics[width=\twidth]{eps/blackmanHarris3Long}](http://www.dsprelated.com/josimages_new/sasp2/img421.png)











