Free Books
   Free Books    Spectral Audio Signal Processing  

Cyclic Autocorrelation

For sequences of length $ N$ , the cyclic autocorrelation operator is defined by

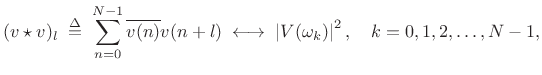$\displaystyle (v\star v)_l \isdefs \sum_{n=0}^{N-1} \overline{v(n)} v(n+l) \;\longleftrightarrow\;\left\vert V(\omega_k)\right\vert^2, \quad k=0,1,2,\ldots,N-1,$ (7.19)

where 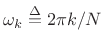$ \omega_k\isdef 2\pi k/N$ and the index $ n+l$ is interpreted modulo $ N$ .

By using zero padding by a factor of 2 or more, cyclic autocorrelation also implements acyclic autocorrelation as defined in (6.16).

An unbiased cyclic autocorrelation is obtained, in the zero-mean case, by simply normalizing $ v\star v$ by the number of terms in the sum:

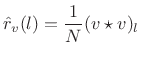$\displaystyle \hat{r}_v(l) = \frac{1}{N}(v\star v)_l$ (7.20)

Next Section:
Practical Bottom Line
Previous Section:
Smoothed Power Spectral Density