Biased Sample Autocorrelation
The sample autocorrelation defined in (6.6) is not quite
the same as the autocorrelation function for infinitely long
discrete-time sequences defined in §2.3.6,
viz.,
where the signal
Thus,
It is common in practice to retain the implicit Bartlett (triangular) weighting in the sample autocorrelation. It merely corresponds to smoothing of the power spectrum (or cross-spectrum) with the
The left column of Fig.6.1 in fact shows the Bartlett-biased sample autocorrelation. When the bias is removed, the autocorrelation appears noisier at higher lags (near the endpoints of the plot).
Next Section:
Smoothed Power Spectral Density
Previous Section:
Sample Power Spectral Density








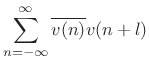
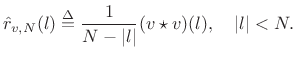
![$\displaystyle (v\star v)(l) = \left\{\begin{array}{ll} (N-\left\vert l\right\vert) \hat{r}_{v,N}(l), & l=0,\pm1,\pm2,\ldots,\pm (N-1) \\ [5pt] 0, & \vert l\vert\geq N. \\ \end{array} \right. \protect$](http://www.dsprelated.com/josimages_new/sasp2/img1137.png)











