Practical Bottom Line
Since we must use the DFT in practice, preferring an FFT for speed,
we typically compute the sample autocorrelation function for a
length ![]() sequence
sequence ![]() ,
,
![]() as follows:
as follows:
- Choose the FFT size
 to be a power of 2
providing at least
to be a power of 2
providing at least 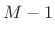 samples of zero padding
(
samples of zero padding
(
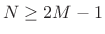 ):
):
![$\displaystyle x \isdef [v(0),v(1),\ldots,v(M-1), \underbrace{0,\ldots,0}_{\hbox{$N-M$}}].$](http://www.dsprelated.com/josimages_new/sasp2/img1148.png)
(7.21)
- Perform a length
 FFT to get
FFT to get
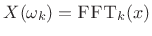 .
.
- Compute the squared magnitude
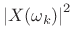 .
.
- Compute the inverse FFT to get
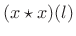 ,
,
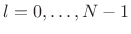 .
.
- Remove the bias, if desired, by inverting the implicit
Bartlett-window weighting to get
![$\displaystyle \hat{r}_{v,M}(l) \isdef \left\{\begin{array}{ll} \frac{1}{M-\vert l\vert} (x\star x)(l), & l=0,\,\pm1,\,\pm2,\,\pm (M-1)\;\mbox{(mod $N$)} \\ [5pt] 0, & \vert l\vert\geq M\; \mbox{(mod $N$)}. \\ \end{array} \right.$](http://www.dsprelated.com/josimages_new/sasp2/img1153.png)
(7.22)
It is important to note that the sample autocorrelation is itself a stochastic process. To stably estimate a true autocorrelation function, or its Fourier transform the power spectral density, many sample autocorrelations (or squared-magnitude FFTs) must be averaged together, as discussed in §6.12 below.
Next Section:
Why an Impulse is Not White Noise
Previous Section:
Cyclic Autocorrelation



















