DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Discrete Wavelet Transform

The discrete wavelet transform is a discrete-time, discrete-frequency counterpart of the continuous wavelet transform of the previous section:

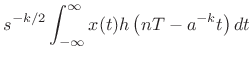$\displaystyle X(k,n)$ $\displaystyle =$ $\displaystyle s^{-k/2} \int_{-\infty}^\infty x(t) h\left(nT-a^{-k}t\right) dt$  
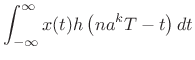  $\displaystyle =$ $\displaystyle \int_{-\infty}^\infty x(t) h\left(na^k T-t\right) dt$  

where $ n$ and $ k$ range over the integers, and $ h$ is the mother wavelet, interpreted here as a (continuous) filter impulse response.

The inverse transform is, as always, the signal expansion in terms of the orthonormal basis set:

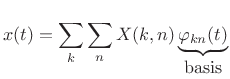$\displaystyle x(t) = \sum_k \sum_n X(k,n) \underbrace{\varphi _{kn}(t)}_{\hbox{basis}}$ (12.120)

We can show that discrete wavelet transforms are constant-Q by defining the center frequency of the $ k$ th basis signal as the geometric mean of its bandlimits $ \omega_1$ and $ \omega _2$ , i.e.,

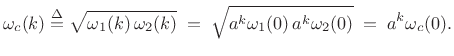$\displaystyle \omega _c(k) \isdef \sqrt{\omega _1(k)\,\omega _2(k)} \eqsp \sqrt{a^k\omega _1(0)\,a^k\omega _2(0)} \eqsp a^k\omega _c(0).$ (12.121)

Then

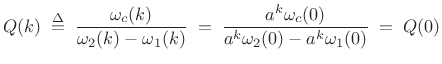$\displaystyle Q(k) \isdefs \frac{\omega _c(k)}{\omega _2(k) - \omega _1(k)} \eqsp \frac{a^k\omega _c(0)}{a^k\omega _2(0) - a^k\omega _1(0)} \eqsp Q(0)$ (12.122)

which does not depend on $ k$ .

Next Section:
Discrete Wavelet Filterbank
Previous Section:
Continuous Wavelet Transform