Dolph-Chebyshev Window Definition

Let denote the desired window length. Then the zero-phase Dolph-Chebyshev window is defined in the frequency domain by [155]

$\displaystyle W(\omega) = \frac{T_{M-1}[x_0 \cos(\omega/2)]}{T_{M-1}(x_0)}$

(4.48)

where is defined by the desired ripple specification:

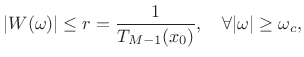$\displaystyle \vert W(\omega)\vert \le r = \frac{1}{T_{M-1}(x_0)}, \quad \forall\vert\omega\vert\ge\omega_c,$

(4.49)

where $\omega_c$ is the ``main lobe edge frequency'' defined by

$\displaystyle \omega_c \isdefs 2\cos^{-1}\left[\frac{1}{x_0}\right].$

(4.50)

Expanding $W(\omega)$ in terms of complex exponentials yields

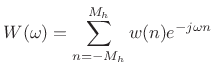$\displaystyle W(\omega) = \sum_{n=-M_h}^{M_h} w(n) e^{-j \omega n}$

(4.51)

where 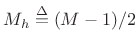$M_h\isdef (M-1)/2$ . Thus, the coefficients give the length Dolph-Chebyshev window in zero-phase form.

Next Section:
Dolph-Chebyshev Window Main-Lobe Width
Previous Section:
Chebyshev Polynomials

Sign in