DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Existence of the Fourier Transform

Conditions for the existence of the Fourier transform are complicated to state in general [36], but it is sufficient for $ x(t)$ to be absolutely integrable, i.e.,

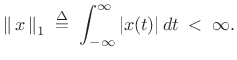$\displaystyle \left\Vert\,x\,\right\Vert _1 \isdefs \int_{-\infty}^\infty \left\vert x(t)\right\vert dt \;<\; \infty .$ (3.6)

This requirement can be stated as $ x\in L1$ , meaning that $ x$ belongs to the set of all signals having a finite $ L1$ norm ( $ \left\Vert\,x\,\right\Vert _1<\infty$ ). It is similarly sufficient for $ x(t)$ to be square integrable, i.e.,

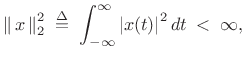$\displaystyle \left\Vert\,x\,\right\Vert _2^2\isdefs \int_{-\infty}^\infty \left\vert x(t)\right\vert^2 dt \;<\; \infty,$ (3.7)

or, $ x\in L2$ . More generally, it suffices to show $ x\in Lp$ for $ 1\leq p\leq 2$ [36, p. 47].

There is never a question of existence, of course, for Fourier transforms of real-world signals encountered in practice. However, idealized signals, such as sinusoids that go on forever in time, do pose normalization difficulties. In practical engineering analysis, these difficulties are resolved using Dirac's ``generalized functions'' such as the impulse (also loosely called the delta function), discussed in §B.10.

Next Section:
Linearity of the DTFT
Previous Section:
Appendices