Free Books
   Free Books    Spectral Audio Signal Processing  

Frequency Envelopes

It is convenient in practice to work with instantaneous frequency deviation instead of phase:

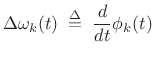$\displaystyle \Delta \omega_k(t) \isdefs \frac{d}{dt} \phi_k(t)$ (G.9)

Since the $ k$ th channel of an $ N$ -channel uniform filter-bank has nominal bandwidth given by $ f_s/N$ , the frequency deviation usually does not exceed $ \pm f_s/(2N)$ .

Note that $ x_k^a(t)$ is a narrow-band signal centered about the channel frequency $ \omega_k$ . As detailed in Chapter 9, it is typical to heterodyne the channel signals to ``base band'' by shifting the input spectrum by $ -\omega_k$ so that the channel bandwidth is centered about frequency zero (dc). This may be expressed by modulating the analytic signal by $ \exp(-j\omega_k t)$ to get

$\displaystyle x_k^b(t) \isdefs e^{-j\omega_k t}\, x_k^a(t) = a_k(t)\, e^{j\phi_k(t)}$ (G.10)

The `b' superscript here stands for ``baseband,'' i.e., the channel-filter frequency-response is centered about dc. Working at baseband, we may compute the frequency deviation as simply the time-derivative of the instantaneous phase of the analytic signal:

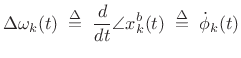$\displaystyle \Delta\omega_k(t) \isdefs \frac{d}{dt} \angle x_k^b(t) \isdefs \dot{\phi}_k(t)$ (G.11)

where

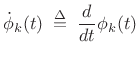$\displaystyle \dot{\phi}_k(t) \isdefs \frac{d}{dt} \phi_k(t)$ (G.12)

denotes the time derivative of $ \phi_k(t)$ . For notational simplicity, let $x(t) \isdeftext \mbox{re\ensuremath{\left\{x_k^b(t)\right\}}}$ and $y(t)\isdeftext \mbox{im\ensuremath{\left\{ x_k^b(t)\right\}}}$ . Then we have

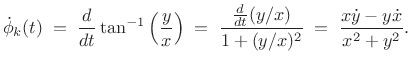$\displaystyle \dot{\phi}_k(t) \eqsp \frac{d}{dt}\tan^{-1}\left(\frac{y}{x}\right) \eqsp \frac{ \frac{d}{dt}{(y/x)}}{ 1+(y/x)^2} \eqsp \frac{x\dot{y}-y\dot{x}}{x^2+y^2} .$ (G.13)

For discrete time, we replace $ t$ by $ n$ to obtain [186]

$\displaystyle \Delta\omega_k(n) \isdefs \dot{\phi}_k(n) \eqsp \frac{x(n)\,\dot{y}(n)-y(n)\,\dot{x}(n)}{x^2(n)+y^2(n)}. \protect$ (G.14)

Initially, the sliding FFT was used (hop size $ R=1$ in the notation of Chapters 8 and 9). Larger hop sizes can result in phase ambiguities, i.e., it can be ambiguous exactly how many cycles of a quasi-sinusoidal component occurred during the hop within a given channel, especially for high-frequency channels. In many applications, this is not a serious problem, as it is only necessary to recreate a psychoacoustically equivalent peak trajectory in the short-time spectrum. For related discussion, see [299].

Using (G.6) and (G.14) to compute the instantaneous amplitude and frequency for each subband, we obtain data such as shown qualitatively in Fig.G.12. A matlab algorithm for phase unwrapping is given in §F.4.1.

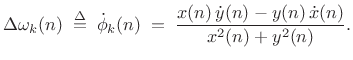
\begin{psfrags} % latex2html id marker 42622\psfrag{ak} []{ \LARGE$ a_k(t)$\ }\psfrag{wkt} []{ \LARGE$ \Delta\omega_k(t)=\dot{\phi_k}(t) $\ }\psfrag{wk} []{ \LARGE$ 0 $\ }\psfrag{t} []{ \LARGE$ t$\ }\begin{figure}[htbp] \includegraphics[width=3.5in]{eps/traj} \caption{Example amplitude envelope (top) and frequency envelope (bottom).} \end{figure} \end{psfrags}

Next Section:
Envelope Compression
Previous Section:
Further Reading about FM Synthesis