Gaussian Probability Density Function
Any non-negative function which integrates to 1 (unit total area) is suitable for use as a probability density function (PDF) (§C.1.3). The most general Gaussian PDF is given by shifts of the normalized Gaussian:
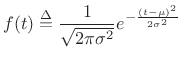 |
(D.28) |
The parameter
Next Section:
Maximum Entropy Property of the Gaussian Distribution
Previous Section:
Why Gaussian?




















