Why Gaussian?
This section lists some of the points of origin for the Gaussian function in mathematics and physics.
Central Limit Theorem
The central limit theoremD.2provides that many iterated convolutions of any ``sufficiently regular'' shape will approach a Gaussian function.
Iterated Convolutions
Any ``reasonable'' probability density function (PDF) (§C.1.3)
has a Fourier transform that looks like
near its tip. Iterating 
convolutions then corresponds to
, which becomes
[2]
 |
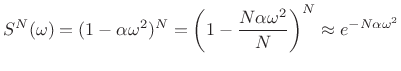(D.27) |
for large
, by the definition of 
[264]. This proves that
the
th power of
approaches the Gaussian function
defined in §D.1 for large
.
Since the inverse Fourier transform of a Gaussian is another Gaussian
(§D.8), we can define a time-domain function 
as
being ``sufficiently regular'' when its Fourier transform approaches
in a sufficiently small
neighborhood of 
. That is, the Fourier transform simply
needs a ``sufficiently smooth peak'' at
that can be
expanded into a convergent Taylor series. This obviously holds for
the DTFT of any discrete-time window function 
(the subject of
Chapter 3), because the window transform 
is a finite
sum of continuous cosines of the form
in the
zero-phase case, and complex exponentials in the causal case, each of
which is differentiable any number of times in 
.
Binomial Distribution
The last row of Pascal's triangle (the binomial distribution) approaches a sampled Gaussian function as the number of rows increases.D.3 Since Lagrange interpolation (elementary polynomial interpolation) is equal to binomially windowed sinc interpolation [301,134], it follows that Lagrange interpolation approaches Gaussian-windowed sinc interpolation at high orders.
Next Section:
Gaussian Probability Density Function
Previous Section:
Fourier Transform of Complex Gaussian
