DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Gaussian Window and Transform

The Gaussian ``bell curve'' is possibly the only smooth, nonzero function, known in closed form, that transforms to itself.4.15

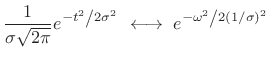$\displaystyle \frac{1}{\sigma\sqrt{2\pi}}e^{-t^2 \left / 2\sigma^2\right.} \;\longleftrightarrow\; e^{-\omega^2 \left/ 2\left(1/\sigma\right)^2\right.}$ (4.55)

It also achieves the minimum time-bandwidth product

$\displaystyle \sigma_t\sigma_\omega = \sigma\times (1/\sigma) = 1$ (4.56)

when ``width'' is defined as the square root of its second central moment. For even functions $ w(t)$ ,

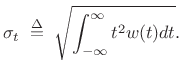$\displaystyle \sigma_t \isdefs \sqrt{\int_{-\infty}^\infty t^2 w(t) dt}.$ (4.57)

Since the true Gaussian function has infinite duration, in practice we must window it with some usual finite window, or truncate it.

Depalle [58] suggests using a triangular window raised to some power $ \alpha $ for this purpose, which preserves the absence of side lobes for sufficiently large $ \alpha $ . It also preserves non-negativity of the transform.

Matlab for the Gaussian Window

In matlab, w = gausswin(M,alpha) returns a length $ M$ window with parameter $ \texttt{alpha} \isdeftext 1/\tilde{\sigma}$ where $ \tilde{\sigma}\isdeftext \sigma/((M-1)/2)$ is defined, as in Harris [101], so that the window shape is invariant with respect to window length $ M$ :

function [w] = gausswin(M,alpha)
n = -(M-1)/2 : (M-1)/2;
w = exp((-1/2) * (alpha * n/((M-1)/2)) .^ 2)';

An implementation in terms of unnormalized standard deviation (sigma in samples) is as follows:

function [w] = gaussianwin(M,sigma)
n= -(M-1)/2 : (M-1)/2;
w = exp(-n .* n / (2 * sigma * sigma))';
In this case, sigma would normally be specified as a fraction of the window length $ M$ (sigma = M/8 in the sample below).

Note that, on a dB scale, Gaussians are quadratic. This means that parabolic interpolation of a sampled Gaussian transform is exact. This can be a useful fact to remember when estimating sinusoidal peak frequencies in spectra. For example, one suggested implication is that, for typical windows, quadratic interpolation of spectral peaks may be more accurate on a log-magnitude scale (e.g., dB) than on a linear magnitude scale (this has been observed empirically for a variety of cases).

Gaussian Window and Transform

Figure 3.36 shows an example length $ M=21$ Gaussian window and its transform. The sigma parameter was set to $ M/8$ so that simple truncation of the Gaussian yields a side-lobe level better than $ -80$ dB. Also overlaid on the window transform is a parabola; we see that the main lobe is well fit by the parabola until the side lobes begin. Since the transform of a Gaussian is a Gaussian (exactly), the side lobes are entirely caused by truncating the window.

Figure 3.36: Gaussian window and transform.
\includegraphics[width=\twidth]{eps/gaussianWindow}

More properties and applications of the Gaussian function can be found in Appendix D.

Exact Discrete Gaussian Window

It can be shown [44] that

$\displaystyle e^{-j\frac{\pi}{8}} \, e^{j\frac{2\pi}{N}\frac{1}{2}n^2} \;\longleftrightarrow\; e^{j\frac{\pi}{8}} \, e^{-j\frac{2\pi}{N}\frac{1}{2}k^2}$ (4.58)

where $ n\in[0,N-1]$ is the time index, and $ k\in[0,N-1]$ is the frequency index for a length $ N$ (even) normalized DFT (DFT divided by $ \sqrt{N}$ ). In other words, the Normalized DFT (NDFT) of this particular sampled Gaussian pulse is exactly the complex-conjugate of the same Gaussian pulse. (The proof is nontrivial.)

Next Section:
Optimized Windows
Previous Section:
Dolph-Chebyshev Window