Generalized STFT

Free Books Spectral Audio Signal Processing

A generalized STFT may be defined by [287]

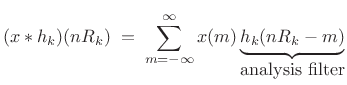$\displaystyle x_k(n)$	$\displaystyle =$	$\displaystyle (x\ast h_k)(nR_k) \eqsp \sum_{m=-\infty}^{\infty}x(m) \underbrace{h_k(nR_k - m)}_{\hbox{analysis filter}}$
$\displaystyle x(n)$	$\displaystyle =$	$\displaystyle \sum_k (x_k\ast f_k)(n) \eqsp \sum_{k=0}^{N-1}\sum_{m=-\infty}^{\infty}x_k(m) \underbrace{f_k(n-m R_k)}_{\hbox{synthesis filter}}$

This filter bank and its reconstruction are diagrammed in Fig.11.35.

**Figure 11.35:** Generalized STFT
$\includegraphics[width=\twidth]{eps/GenSTFT}$

The analysis filter is typically complex bandpass (as in the STFT case). The integers give the downsampling factor for the output of the th channel filter: For critical sampling without aliasing, we set $R_k= \pi/\hbox{Width}(H_k)$ . The impulse response of synthesis filter can be regarded as the th basis signal in the reconstruction. If the $\{f_k\}$ are orthonormal, then we have $f_k(n) = h_k^\ast(-n)$ . More generally, $\{h_k,f_k\}$ form a biorthogonal basis.