DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Under the Hood of kaiserord

Without kaiserord, we would need to implement Kaiser's formula [115,67] for estimating the Kaiser-window $ \beta $ required to achieve the given filter specs:

$\displaystyle \beta = \left\{\begin{array}{ll} 0.1102(A-8.7), & A > 50 \\ [5pt] 0.5842(A-21)^{0.4} + 0.07886(A-21), & 21< A < 50 \\ [5pt] 0, & A < 21, \\ \end{array} \right. \protect$ (5.11)

where $ A$ is the desired stop-band attenuation in dB (typical values in audio work are $ A=60$ to $ 90$ ). Note that this estimate for $ \beta $ becomes too small when the filter pass-band width approaches zero. In the limit of a zero-width pass-band, the frequency response becomes that of the Kaiser window transform itself. A non-zero pass-band width acts as a ``moving average'' lowpass filter on the side-lobes of the window transform, which brings them down in level. The kaiserord estimate assumes some of this side-lobe smoothing is present.

A similar function from [198] for window design (as opposed to filter design5.7) is

$\displaystyle \beta = \left\{\begin{array}{ll} 0, & A<13.26 \\ [5pt] 0.76609(A-13.26)^{0.4} + 0.09834(A-13.26), & 13.26< A < 60 \\ [5pt] 0.12438*(A+6.3), & 60<A<120, \\ \end{array} \right. \protect$ (5.12)

where now $ A$ is the desired side-lobe attenuation in dB (as opposed to stop-band attenuation). A plot showing Kaiser window side-lobe level for various values of $ \beta $ is given in Fig.3.28.

Similarly, the filter order $ M$ is estimated from stop-band attenuation $ A$ and desired transition width $ \Delta\omega$ using the empirical formula

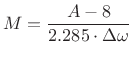$\displaystyle M = \frac{A-8}{2.285 \cdot \Delta\omega}$ (5.13)

where $ \Delta\omega$ is in radians between 0 and $ \pi$ .

Without the function fir1, we would have to manually implement the window method of filter design by (1) constructing the impulse response of the ideal bandpass filter $ h(n)$ (a cosine modulated sinc function), (2) computing the Kaiser window $ w(n)$ using the estimated length and $ \beta $ from above, then finally (3) windowing the ideal impulse response with the Kaiser window to obtain the FIR filter coefficients $ h_w(n) = w(n)h(n)$ . A manual design of this nature will be illustrated in the Hilbert transform example of §4.6.

Next Section:
Comparison to the Optimal Chebyshev FIR Bandpass Filter
Previous Section:
Convergence of Remez Exchange