Hilbert Transform Design Example
We will now use the window method to design a complex bandpass filter which passes positive frequencies and rejects negative frequencies.
Since every real signal ![]() possesses a Hermitian spectrum
possesses a Hermitian spectrum
![]() , i.e.,
, i.e.,
![]() , it follows that, if
we filter out the negative frequencies, we will destroy this spectral
symmetry, and the output signal will be complex for every nonzero real
input signal (excluding dc and half the sampling rate). In other
terms, we want a filter which produces a ``single sideband'' (SSB)
output signal in response to any real input signal. The Hermitian
spectrum of a real signal can be viewed as two sidebands about
dc (with one sideband being the ``conjugate flip'' of the other). See
§2.3.3 for a review of Fourier symmetry-properties for
real signals.
, it follows that, if
we filter out the negative frequencies, we will destroy this spectral
symmetry, and the output signal will be complex for every nonzero real
input signal (excluding dc and half the sampling rate). In other
terms, we want a filter which produces a ``single sideband'' (SSB)
output signal in response to any real input signal. The Hermitian
spectrum of a real signal can be viewed as two sidebands about
dc (with one sideband being the ``conjugate flip'' of the other). See
§2.3.3 for a review of Fourier symmetry-properties for
real signals.
An ``analytic signal'' in signal processing is defined as any
signal ![]() having only positive or only negative frequencies, but
not both (typically only positive frequencies). In principle, the
imaginary part of an analytic signal is computed from its real part by
the Hilbert transform (defined and discussed below). In other
words, one can ``filter out'' the negative-frequency components of a
signal
having only positive or only negative frequencies, but
not both (typically only positive frequencies). In principle, the
imaginary part of an analytic signal is computed from its real part by
the Hilbert transform (defined and discussed below). In other
words, one can ``filter out'' the negative-frequency components of a
signal ![]() by taking its Hilbert transform
by taking its Hilbert transform
![]() and forming the analytic signal
and forming the analytic signal
![]() . Thus, an
alternative problem specification is to ask for a (real) filter which
approximates the Hilbert transform as closely as possible for a given
filter order.
. Thus, an
alternative problem specification is to ask for a (real) filter which
approximates the Hilbert transform as closely as possible for a given
filter order.
Primer on Hilbert Transform Theory
We need a Hilbert-transform filter ![]() to compute the imaginary
part
to compute the imaginary
part ![]() of the analytic signal
of the analytic signal ![]() given its real part
given its real part
![]() . That is,
. That is,
| (5.14) |
where
| (5.15) |
where
In view of the foregoing, the frequency response of the ideal Hilbert-transform filter may be defined as follows:
Note that the point at
The ideal filter impulse response ![]() is obtained by finding the
inverse Fourier transform of (4.16). For discrete time, we may
take the inverse DTFT of (4.16) to obtain the ideal discrete-time
Hilbert-transform impulse response, as pursued in Problem 10.
We will work with the usual continuous-time limit
is obtained by finding the
inverse Fourier transform of (4.16). For discrete time, we may
take the inverse DTFT of (4.16) to obtain the ideal discrete-time
Hilbert-transform impulse response, as pursued in Problem 10.
We will work with the usual continuous-time limit
![]() in
the next section.
in
the next section.
Hilbert Transform
The Hilbert transform ![]() of a real, continuous-time signal
of a real, continuous-time signal
![]() may be expressed as the convolution of
may be expressed as the convolution of ![]() with the
Hilbert transform kernel:
with the
Hilbert transform kernel:
That is, the Hilbert transform of
| (5.18) |
Thus, the Hilbert transform is a non-causal linear time-invariant filter.
The complex analytic signal ![]() corresponding to the real signal
corresponding to the real signal ![]() is
then given by
is
then given by
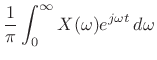 |
(5.19) |
To show this last equality (note the lower limit of 0
instead of the
usual ![]() ), it is easiest to apply (4.16) in the frequency
domain:
), it is easiest to apply (4.16) in the frequency
domain:
| (5.20) | |||
| (5.21) |
Thus, the negative-frequency components of
Filtering and Windowing the Ideal
Hilbert-Transform Impulse Response
Let ![]() denote the convolution kernel of the continuous-time
Hilbert transform from (4.17) above:
denote the convolution kernel of the continuous-time
Hilbert transform from (4.17) above:
Convolving a real signal
Note that we cannot allow a time-domain sample at time 0 in (4.22) because it would be infinity. Instead, time 0 should be taken to lie between two samples, thereby introducing a small non-integer advance or delay. We'll choose a half-sample delay. As a result, we'll need to delay the real-part filter by half a sample as well when we make a complete single-sideband filter.
The matlab below illustrates the design of an FIR Hilbert-transform
filter by the window method using a Kaiser window. For a more
practical illustration, the sampling-rate assumed is set to
![]() Hz instead of being normalized to 1 as usual. The
Kaiser-window
Hz instead of being normalized to 1 as usual. The
Kaiser-window ![]() parameter is set to
parameter is set to ![]() , which normally gives
``pretty good'' audio performance (cf. Fig.3.28). From
Fig.3.28, we see that we can expect a stop-band attenuation
better than
, which normally gives
``pretty good'' audio performance (cf. Fig.3.28). From
Fig.3.28, we see that we can expect a stop-band attenuation
better than ![]() dB. The choice of
dB. The choice of ![]() , in setting the
time-bandwidth product of the Kaiser window, determines both the
stop-band rejection and the transition bandwidths required by our FIR
frequency response.
, in setting the
time-bandwidth product of the Kaiser window, determines both the
stop-band rejection and the transition bandwidths required by our FIR
frequency response.
M = 257; % window length = FIR filter length (Window Method) fs = 22050; % sampling rate assumed (Hz) f1 = 530; % lower pass-band limit = transition bandwidth (Hz) beta = 8; % beta for Kaiser window for decent side-lobe rejectionRecall that, for a rectangular window, our minimum transition bandwidth would be
Matlab, Continued
Given the above design parameters, we compute some derived parameters as follows:
fn = fs/2; % Nyquist limit (Hz) f2 = fn - f1; % upper pass-band limit N = 2^(nextpow2(8*M)); % large FFT for interpolated display k1 = round(N*f1/fs); % lower band edge in bins if k1<2, k1=2; end; % cannot have dc or fn response kn = N/2 + 1; % bin index at Nyquist limit (1-based) k2 = kn-k1+1; % high-frequency band edge f1 = k1*fs/N % quantized band-edge frequencies f2 = k2*fs/NSetting the upper transition band the same as the low-frequency band (
Kaiser Window
With the filter length ![]() and Kaiser window
and Kaiser window ![]() as given
above, we may compute the Kaiser window itself in matlab via
as given
above, we may compute the Kaiser window itself in matlab via
w = kaiser(M,beta)'; % Kaiser window in "linear phase form"The spectrum of this window (zero-padded by more than a factor of 8) is shown in Fig.4.9 (full magnitude spectrum) and Fig.4.10 (zoom-in on the main lobe).
Windowing a Desired Impulse Response Computed by the
Frequency Sampling Method
The next step is to apply our Kaiser window to the ``desired'' impulse
response, where ``desired'' means a time-shifted (by 1/2 sample) and
bandlimited (to introduce transition bands) version of the ``ideal''
impulse response in (4.22). In principle, we are using the
frequency-sampling method (§4.4) to prepare a
desired FIR filter of length ![]() as the inverse FFT of a desired
frequency response prepared by direct Fourier intuition. This long
FIR filter is then ``windowed'' down to length
as the inverse FFT of a desired
frequency response prepared by direct Fourier intuition. This long
FIR filter is then ``windowed'' down to length ![]() to give us our
final FIR filter designed by the window method.
to give us our
final FIR filter designed by the window method.
If the smallest transition bandwidth is ![]() Hz, then the FFT size
Hz, then the FFT size ![]() should satisfy
should satisfy
![]() . Otherwise, there may be too much time
aliasing in the desired impulse response.5.10 The only non-obvious
part in the matlab below is ``
. Otherwise, there may be too much time
aliasing in the desired impulse response.5.10 The only non-obvious
part in the matlab below is ``.^8'' which smooths the taper to
zero and looks better on a log magnitude scale. It would also make
sense to do a linear taper on a dB scale which corresponds to
an exponential taper to zero.
H = [ ([0:k1-2]/(k1-1)).^8,ones(1,k2-k1+1),...
([k1-2:-1:0]/(k1-1)).^8, zeros(1,N/2-1)];
Figure 4.11 shows our desired amplitude response so constructed.
Now we inverse-FFT the desired frequency response to obtain the desired impulse response:
h = ifft(H); % desired impulse response hodd = imag(h(1:2:N)); % This should be zero ierr = norm(hodd)/norm(h); % Look at numerical round-off error % Typical value: ierr = 4.1958e-15 % Also look at time aliasing: aerr = norm(h(N/2-N/32:N/2+N/32))/norm(h); % Typical value: 4.8300e-04The real part of the desired impulse response is shown in Fig.4.12, and the imaginary part in Fig.4.13.
Now use the Kaiser window to time-limit the desired impulse response:
% put window in zero-phase form: wzp = [w((M+1)/2:M), zeros(1,N-M), w(1:(M-1)/2)]; hw = wzp .* h; % single-sideband FIR filter, zero-centered Hw = fft(hw); % for results display: plot(db(Hw)); hh = [hw(N-(M-1)/2+1:N),hw(1:(M+1)/2)]; % caual FIR % plot(db(fft([hh,zeros(1,N-M)]))); % freq resp plot
Figure 4.14 and Fig.4.15
show the normalized dB magnitude frequency response of our
final FIR filter consisting of the ![]() nonzero samples of
hw.
nonzero samples of
hw.
More General FIR Filter Design
We have looked at more than just FIR filter design by the window method and frequency-sampling technique. The general steps were
- Prepare a desired frequency-response that ``seems achievable''
- Inverse FFT
- Window the result (time-limit it)
- FFT that to see how it looks
Comparison to Optimal Chebyshev FIR Filter
Let's now compare the window-method design using the Kaiser window to the optimal equiripple FIR filter design given by the Remez multiple exchange algorithm.
Note, by the way, that many filter-design software functions, such as firpm have special modes for designing Hilbert-transform filters [224].
It turns out that the Remez exchange algorithm has convergence
problems for filters larger than a few hundred taps. Therefore, the
FIR filter length ![]() was chosen above to be small enough to work
out in this comparison. However, keep in mind that for very large
filter orders, the Remez exchange method may not be an option. There
are more recently developed methods for optimal Chebyshev FIR filter
design, using ``convex optimization'' techniques, that may continue to
work at very high orders
[218,22,153]. The fast nonparametric
methods discussed above (frequency sampling, window method) will work
fine at extremely high orders.
was chosen above to be small enough to work
out in this comparison. However, keep in mind that for very large
filter orders, the Remez exchange method may not be an option. There
are more recently developed methods for optimal Chebyshev FIR filter
design, using ``convex optimization'' techniques, that may continue to
work at very high orders
[218,22,153]. The fast nonparametric
methods discussed above (frequency sampling, window method) will work
fine at extremely high orders.
The following Matlab command will try to design the FIR Hilbert-transform filter of the desired length with the desired transition bands:
hri = firpm(M-1, [f1,f2]/fn, [1,1], [1], 'Hilbert');Instead, however, we will use a more robust method [228] which uses the Remez exchange algorithm to design a lowpass filter, followed by modulation of the lowpass impulse-response by a complex sinusoid at frequency
tic; % remember the current time hrm = firpm(M-1, [0,(f2-fs/4)/fn,0.5,1], [1,1,0,0], [1,10]); dt = toc; % design time dt can be minutes hr = hrm .* j .^ [0:M-1]; % modulate lowpass to single-sidebandThe weighting [1,10] in the call to firpm above says ``make the pass-band ripple
![\includegraphics[width=0.8\twidth]{eps/OptimalHilbertFR}](http://www.dsprelated.com/josimages_new/sasp2/img802.png) |
In this case we did not normalize the peak amplitude response to 0 dB because it has a ripple peak of about 1 dB in the pass-band. Figure 4.18 shows a zoom-in on the pass-band ripple.
Conclusions
We can note the following points regarding our single-sideband FIR filter design by means of direct Fourier intuition, frequency-sampling, and the window-method:
- The pass-band ripple is much smaller than 0.1 dB, which is
``over designed'' and therefore wasting of taps.
- The stop-band response ``droops'' which ``wastes'' filter taps
when stop-band attenuation is the only stop-band specification. In
other words, the first stop-band ripple drives the spec (
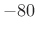 dB),
while all higher-frequency ripples are over-designed. On the other
hand, a high-frequency ``roll-off'' of this nature is quite natural
in the frequency domain, and it corresponds to a ``smoother pulse''
in the time domain. Sometimes making the stop-band attenuation
uniform will cause small impulses at the beginning and end of
the impulse response in the time domain. (The pass-band and
stop-band ripple can ``add up'' under the inverse Fourier transform
integral.) Recall this impulsive endpoint phenomenon for the
Chebyshev window shown in Fig.3.33.
dB),
while all higher-frequency ripples are over-designed. On the other
hand, a high-frequency ``roll-off'' of this nature is quite natural
in the frequency domain, and it corresponds to a ``smoother pulse''
in the time domain. Sometimes making the stop-band attenuation
uniform will cause small impulses at the beginning and end of
the impulse response in the time domain. (The pass-band and
stop-band ripple can ``add up'' under the inverse Fourier transform
integral.) Recall this impulsive endpoint phenomenon for the
Chebyshev window shown in Fig.3.33.
- The pass-band is degraded by early roll-off. The pass-band edge
is not exactly in the desired place.
- The filter length can be thousands of taps long without running
into numerical failure. Filters this long are actually needed for
sampling rate conversion
[270,218].
We can also note some observations regarding the optimal Chebyshev version designed by the Remez multiple exchange algorithm:
- The stop-band is ideal, equiripple.
- The transition bandwidth is close to half that of the
window method. (We already knew our chosen transition bandwidth was
not ``tight'', but our rule-of-thumb based on the Kaiser-window
main-lobe width predicted only about
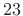 % excess width.)
% excess width.)
- The pass-band is ideal, though over-designed for static audio spectra.
- The computational design time is orders of magnitude larger
than that for window method.
- The design fails to converge for filters much longer than 256
taps. (Need to increase working precision or use a different
method to get longer optimal Chebyshev FIR filters.)
Next Section:
Generalized Window Method
Previous Section:
Window Method for FIR Filter Design








![$\displaystyle H(\omega) \isdefs \left\{\begin{array}{ll} \quad\! j, & \omega<0 \\ [5pt] \quad\!0, & \omega=0 \\ [5pt] -j, & \omega>0 \\ \end{array} \right. \protect$](http://www.dsprelated.com/josimages_new/sasp2/img760.png)
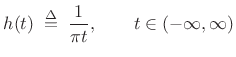
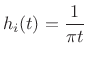
![\includegraphics[width=0.8\twidth]{eps/KaiserFR}](http://www.dsprelated.com/josimages_new/sasp2/img792.png)
![\includegraphics[width=0.8\twidth]{eps/KaiserZoomFR}](http://www.dsprelated.com/josimages_new/sasp2/img793.png)
![\includegraphics[width=0.8\twidth]{eps/hilbertFRIdeal}](http://www.dsprelated.com/josimages_new/sasp2/img796.png)
![\includegraphics[width=0.8\twidth]{eps/hilbertIRRealIdeal}](http://www.dsprelated.com/josimages_new/sasp2/img797.png)
![\includegraphics[width=0.8\twidth]{eps/hilbertIRImagIdeal}](http://www.dsprelated.com/josimages_new/sasp2/img798.png)
![\includegraphics[width=0.8\twidth]{eps/KaiserHilbertFR}](http://www.dsprelated.com/josimages_new/sasp2/img799.png)
![\includegraphics[width=0.8\twidth]{eps/KaiserHilbertZoomedFR}](http://www.dsprelated.com/josimages_new/sasp2/img800.png)
![\includegraphics[width=0.8\twidth]{eps/OptimalHilbertZoomedFR}](http://www.dsprelated.com/josimages_new/sasp2/img803.png)
![\includegraphics[width=0.8\twidth]{eps/OptimalHilbertZoomedPB}](http://www.dsprelated.com/josimages_new/sasp2/img804.png)











