DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Infinite Flatness at Infinity

The Gaussian is infinitely flat at infinity. Equivalently, the Maclaurin expansion (Taylor expansion about $ t=0$ ) of

$\displaystyle f(t) = e^{-\frac{1}{t^2}}$ (D.3)

is zero for all orders. Thus, even though $ f(t)$ is differentiable of all orders at $ t=0$ , its series expansion fails to approach the function. This happens because $ e^{t^2}$ has an essential singularity at $ t=\infty$ (also called a ``non-removable singularity''). One can think of an essential singularity as an infinite number of poles piled up at the same point ($ t=\infty$ for $ e^{t^2}$ ). Equivalently, $ f(t)$ above has an infinite number of zeros at $ t=0$ , leading to the problem with Maclaurin series expansion. To prove this, one can show

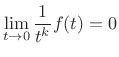$\displaystyle \lim_{t\to 0} \frac{1}{t^k} f(t) = 0$ (D.4)

for all $ k=1,2,\dots\,$ . This follows from the fact that exponential growth or decay is faster than polynomial growth or decay. An exponential can in fact be viewed as an infinite-order polynomial, since

$\displaystyle e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots.$ (D.5)

We may call $ f(t) = e^{-\frac{1}{t^2}}$ infinitely flat at $ t=0$ in the ``Padé sense'':

Another interesting mathematical property of essential singularities is that near an essential singular point $ z_0\in{\bf C}$ the inequality

$\displaystyle \left\vert f(z)-c\right\vert<\epsilon$ (D.6)

is satisfied at some point $ z\neq z_0$ in every neighborhood of $ z_0$ , however small. In other words, $ f(z)$ comes arbitrarily close to every possible value in any neighborhood about an essential singular point. This was first proved by Weierstrass [42, p. 270].

Next Section:
Integral of a Complex Gaussian
Previous Section:
Fitting a Gaussian to Data