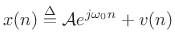DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Maximum Likelihood Sinusoid Estimation

The maximum likelihood estimator (MLE) is widely used in practical signal modeling [121]. A full treatment of maximum likelihood estimators (and statistical estimators in general) lies beyond the scope of this book. However, we will show that the MLE is equivalent to the least squares estimator for a wide class of problems, including well resolved sinusoids in white noise.

Consider again the signal model of (5.32) consisting of a complex sinusoid in additive white (complex) noise:

$\displaystyle x(n) \isdef {\cal A}e^{j\omega_0 n} + v(n) \protect$ (6.44)

Again, $ {\cal A}= A e^{j\phi}$ is the complex amplitude of the sinusoid, and $ v(n)$ is white noise. In addition to assuming $ v$ is white, we add the assumption that it is Gaussian distributed6.12 with zero mean; that is, we assume that its probability density function (see Appendix C) is given by6.13

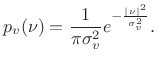$\displaystyle p_v(\nu) = \frac{1}{\pi \sigma_v^2} e^{-\frac{\vert\nu\vert^2}{\sigma_v^2}}.$ (6.46)

We express the zero-mean Gaussian assumption by writing

$\displaystyle v(n) \sim {\cal N}(0,\sigma_v^2).$ (6.47)

The parameter $ \sigma_v^2$ is called the variance of the random process $ v(n)$ , and $ \sigma_v$ is called the standard deviation.

It turns out that when Gaussian random variables $ v(n)$ are uncorrelated (i.e., when $ v(n)$ is white noise), they are also independent. This means that the probability of observing particular values of $ v(n)$ and $ v(m)$ is given by the product of their respective probabilities [121]. We will now use this fact to compute an explicit probability for observing any data sequence $ x(n)$ in (5.44).

Since the sinusoidal part of our signal model, $ {\cal A}e^{j\omega_0 n}$ , is deterministic; i.e., it does not including any random components; it may be treated as the time-varying mean of a Gaussian random process $ x(n)$ . That is, our signal model (5.44) can be rewritten as

$\displaystyle x(n) \sim {\cal N}({\cal A}e^{j\omega_0 n},\sigma_v^2)$ (6.48)

and the probability density function for the whole set of observations $ x(n)$ , $ n=0,1,2,\ldots,N-1$ is given by

$\displaystyle p(x) = p[x(0)] p[x(1)]\cdots p[x(N-1)] = \left(\frac{1}{\pi \sigma_v^2}\right)^N e^{-\frac{1}{\sigma_v^2}\sum_{n=0}^{N-1} \left\vert x(n) - {\cal A}e^{j\omega_0 n}\right\vert^2}$ (6.49)

Thus, given the noise variance $ \sigma_v^2$ and the three sinusoidal parameters $ A,\phi,\omega_0 $ (remember that $ {\cal A}= A e^{j\phi}$ ), we can compute the relative probability of any observed data samples $ x(n)$ .

Next Section:
Likelihood Function
Previous Section:
Least Squares Sinusoidal Parameter Estimation